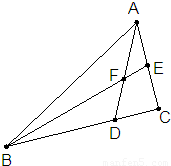
题目内容
 如图在△ABC中,设
如图在△ABC中,设| AB |
| a |
| AC |
| b |
| BD |
| DC |
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| a |
| b |
(1)用
| a |
| b |
| AD |
(2)若点E是AC边的中点,直线BE交AD于F点,求
| AF |
| AB |
分析:(1)利用向量的三角形法则,把
放入三角形中,用其他向量表示,最后,转化到用
,
向量表示即可.
(2)先判断F点分AD的比是多少,可通过过D点作DM∥AC,构造成比例线段,来判断P点的位置,再把
用
表示,根据(1)中结果转化为
,
.计算
•
即可.
| AD |
| a |
| b |
(2)先判断F点分AD的比是多少,可通过过D点作DM∥AC,构造成比例线段,来判断P点的位置,再把
| AF |
| AD |
| a |
| b |
| AF |
| AB |
解答:解:(1)
=
+
=
+
=
+
(
-
)=
+
=
+
(2)过D点作DM∥AC,交BE与点M,∵
=2
,DM∥AC,∴
=
=
又∵点E是AC边的中点,∴
=
∵DM∥AC,∴
=
=
,∴
=
=
(
+
)=
+
,
∴
•
=(
+
)•
=
(|
|)2+
|
||
|cos
=
+
=
| AD |
| AB |
| BD |
| AB |
| 2 |
| 3 |
| BC |
| AB |
| 2 |
| 3 |
| AC |
| AB |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AC |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
(2)过D点作DM∥AC,交BE与点M,∵
| BD |
| DC |
| |DM| |
| |CE| |
| |BD| |
| |BC| |
| 2 |
| 3 |
又∵点E是AC边的中点,∴
| |DM| |
| |AE| |
| 2 |
| 3 |
∵DM∥AC,∴
| |DM| |
| |AE| |
| |DM| |
| AM| |
| 2 |
| 3 |
| AF |
| 3 |
| 5 |
| AD |
| 3 |
| 5 |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
| 1 |
| 5 |
| a |
| 2 |
| 5 |
| b |
∴
| AF |
| AB |
| 1 |
| 5 |
| a |
| 2 |
| 5 |
| b |
| a |
| 1 |
| 5 |
| a |
| 2 |
| 5 |
| a |
| b |
| π |
| 3 |
| 4 |
| 5 |
| 2 |
| 5 |
| 6 |
| 5 |
点评:本题考查了向量的几何运算,做题时应认真分析,找到突破口.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 如图,在△ABC中,设
如图,在△ABC中,设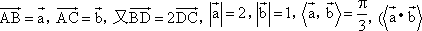 是表示向量
是表示向量 的夹角)
的夹角)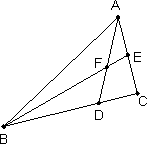

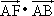
 ,
, .
.
 ;
; 的中点为
的中点为 ,求中线
,求中线 的长.
的长. 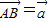 ,
,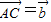 ,又
,又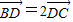 ,
,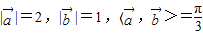 ,(
,(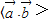 是表示向量
是表示向量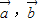 的夹角)
的夹角)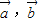 表示
表示
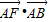 .
.