Question

【题目】在平面直角坐标系中，已知曲线的方程是（，）．

（1）当，时，求曲线围成的区域的面积；

（2）若直线：与曲线交于轴上方的两点，，且，求点到直线距离的最小值．

Answer 1

【答案】(1)4；(2) ．

【解析】

（1）当，时，曲线的方程是，对绝对值内的数进行讨论，得到四条直线围成一个菱形，并求出面积为4；

（2）对进行讨论，化简曲线方程，并与直线方程联立，求出点的坐标，由得到的关系，再利用点到直线的距离公式求出，从而求得.

（1）当，时，曲线的方程是，

当时，，当时，，

当时，方程等价于，

当时，方程等价于，

当时，方程等价于，

当时，方程等价于，

曲线围成的区域为菱形，其面积为；

（2）当，时，有，

联立直线可得，

当，时，有，

联立直线可得，

由可得，

即有，

化为，

点到直线距离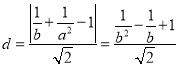

，

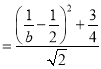由题意可得，，，即，

可得，，

可得当，即时，点到直线距离取得最小值．