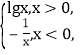题目内容
【题目】已知曲线C的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() (
(![]() 为参数,0≤α<π).
为参数,0≤α<π).
(1)求曲线C的直角坐标方程.并说明曲线C的形状;
(2)若直线l经过点M(1,0)且与曲线C交于A、B两点,求|AB|.
【答案】(1)y2=4x,曲线C是抛物线.(2)8
【解析】
(1)运用x=ρcosθ,y=ρsinθ,即可将曲线C的极坐标方程化为直角坐标方程;
(2)化直线的参数方程为普通方程,再由条件,即可得到斜率,再联立抛物线方程,消去x,得到y的方程,运用韦达定理和弦长公式,即可得到所求值.
解:(1)对于曲线C:![]() 可化为
可化为![]() ,
,
把互化公式代入,得y=![]() ,
,
∴曲线C的直角坐标方程为y2=4x,
曲线C是抛物线.
(2)根据条件直线l经过两定点(1,0)和(0,1),
∴其方程为x+y=1.
由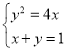 ,消去x并整理得:y2+4y-4=0,
,消去x并整理得:y2+4y-4=0,
令A(x1,y1),B(x2,y2),
则y1+y2=-4,y1y2=-4,
∴|AB|=![]()
![]() =
=![]() =8
=8

练习册系列答案
相关题目