Question

设A={x∈R|x²+4x-5=0},B={x∈R|x²+2ax-2a²+3=0,a∈R},

(1)若A∩B=B,求实数a的范围;

(2)若A∩B=A,求实数a的值.

Answer 1

解：(1)由已知得A={-5,1},∵A∩B=B,∴BA.则B可能有,{-5},{1},{-5,1}四种情况.

①当B=时,方程x²+2ax-2a²+3=0无实数解,

∴Δ=4a²-4(-2a²+3)=12(a²-1)＜0,即-1＜a＜1.

②当B={-5}时,Δ=0且(-5)²+2a(-5)-2a²+3=0,a无解,即B≠{-5}.

③当B={1}时,Δ=0且1²+2a-2a²+3=0,解得a=-1.

④当B={-5,1}时,由根与系数的关系有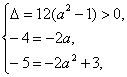解得a=2,

综上可得-1≤a＜1或a=2.

(2)∵A∩B=A,∴AB,

即{-5,1}B.∴B={-5,1}.

由(1)知a=2,即当A∩B=A时,a=2.