题目内容
有以下4个命题:
①A={x∈R|x2+1=0},B={x∈R|4<x<3},则A=B.
②已知函数f(x)是偶函数,而且在(0,+∞)上增函数,则在(-∞,0)上也是增函数.;
③函数f(x)=x2-(k2+3k+9)x+2(k是实常数)在区间(-∞,-2010)是减函数.
④设f(x)=
,g(x)=
,则g(2x)=[f(x)]2+[g(x)]2.
其中正确的命题序号是
①A={x∈R|x2+1=0},B={x∈R|4<x<3},则A=B.
②已知函数f(x)是偶函数,而且在(0,+∞)上增函数,则在(-∞,0)上也是增函数.;
③函数f(x)=x2-(k2+3k+9)x+2(k是实常数)在区间(-∞,-2010)是减函数.
④设f(x)=
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
其中正确的命题序号是
③④
③④
.分析:①A={x∈R|x2+1=0}=∅,B={x∈R|4<x<3},则A≠B;
②已知函数f(x)是偶函数,而且在(0,+∞)上增函数,则在(-∞,0)上是减函数;
③判断函数f(x)=x2-(k2+3k+9)x+2(k是实常数)的开口及对称轴;
④分别计算出g(2x)与[f(x)]2+[g(x)]2.
②已知函数f(x)是偶函数,而且在(0,+∞)上增函数,则在(-∞,0)上是减函数;
③判断函数f(x)=x2-(k2+3k+9)x+2(k是实常数)的开口及对称轴;
④分别计算出g(2x)与[f(x)]2+[g(x)]2.
解答:解:①由于A={x∈R|x2+1=0}=∅,B={x∈R|4<x<3},则A≠B,故①错;
②由于函数f(x)是偶函数,而且在(0,+∞)上增函数,则在(-∞,0)上是减函数.故②错;
③由于函数f(x)=x2-(k2+3k+9)x+2(k是实常数)开口向上,
且对称轴为x=-
=
x=
=
≥
>-2010
故函数f(x)=x2-(k2+3k+9)x+2在区间(-∞,-2010)是减函数,即③正确;
④由于f(x)=
,g(x)=
,则g(2x)=
,
[f(x)]2+[g(x)]2=
+
=
=g(2x),故④正确.
故答案为 ③④
②由于函数f(x)是偶函数,而且在(0,+∞)上增函数,则在(-∞,0)上是减函数.故②错;
③由于函数f(x)=x2-(k2+3k+9)x+2(k是实常数)开口向上,
且对称轴为x=-
| -(k2+3k+9) |
| 2 |
| k2+3k+9 |
| 2 |
| k2+3k+9 |
| 2 |
(k+
| ||||
| 2 |
| 27 |
| 8 |
故函数f(x)=x2-(k2+3k+9)x+2在区间(-∞,-2010)是减函数,即③正确;
④由于f(x)=
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
| e2x+e-2x |
| 2 |
[f(x)]2+[g(x)]2=
| e2x-2+e-2x |
| 4 |
| e2x+2+e-2x |
| 4 |
| e2x+e-2x |
| 2 |
故答案为 ③④
点评:本题以命题的真假判断为载体考查了函数的奇偶性,函数求值,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
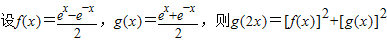 .
. ,则
,则 ;
;