题目内容
已知△ABC的两个顶点A、B分别是椭圆
+
=1 的左、右焦点,三个内角A、B、C满足sinA-sinB=
sinC,则顶点C的轨迹方程是( )
| x2 |
| 25 |
| y2 |
| 9 |
| 1 |
| 2 |
分析:利用正弦定理可把sinA-sinB=
sinC化为|BC|-|AC|=
|AB|,从而判断顶点C是以A、B为焦点的双曲线的左支(除掉与x轴的交点),根据已知条件求出相关量即可求得方程.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:因为A、B是椭圆椭圆
+
=1 的左、右焦点,所以A(-4,0),B(4,0),
由正弦定理得,
=
=
=2R(R为△ABC外接圆的半径),
所以由sinA-sinB=
sinC,得
-
=
•
,即|BC|-|AC|=
|AB|=4<|AB|,
所以顶点C是以A、B为焦点的双曲线的左支(除掉与x轴的交点),
设顶点C的轨迹方程为
-
=1(x<-a),
则a=2,c=4,所以b2=c2-a2=16-4=12,
故顶点C的轨迹方程为
-
=1(x<-2).
故选C.
| x2 |
| 25 |
| y2 |
| 9 |
由正弦定理得,
| |BC| |
| sinA |
| |AC| |
| sinB |
| |AB| |
| sinC |
所以由sinA-sinB=
| 1 |
| 2 |
| |BC| |
| 2R |
| |AC| |
| 2R |
| 1 |
| 2 |
| |AB| |
| 2R |
| 1 |
| 2 |
所以顶点C是以A、B为焦点的双曲线的左支(除掉与x轴的交点),
设顶点C的轨迹方程为
| x2 |
| a2 |
| y2 |
| b2 |
则a=2,c=4,所以b2=c2-a2=16-4=12,
故顶点C的轨迹方程为
| x2 |
| 4 |
| y2 |
| 12 |
故选C.
点评:本题考查圆锥曲线方程的求法及正弦定理的应用,考查学生分析解决问题的能力,本题需注意所求轨迹上的点C为三角形顶点,故与A、B不共线.

练习册系列答案
相关题目
已知△ABC的两个顶点A(-5,0),B(5,0),△ABC的第三个顶点在一条双曲线
-
=1(y≠0)上,则△ABC的内心的轨迹所在图象为( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、两条直线 | B、椭圆 |
| C、双曲线 | D、抛物线 |
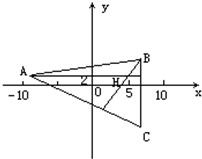 已知△ABC的两个顶点A(-10,2),B(6,4),垂心是H(5,2),求顶点C的坐标.
已知△ABC的两个顶点A(-10,2),B(6,4),垂心是H(5,2),求顶点C的坐标.