题目内容
已知△ABC的两个顶点A(-5,0),B(5,0),△ABC的第三个顶点在一条双曲线
-
=1(y≠0)上,则△ABC的内心的轨迹所在图象为( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、两条直线 | B、椭圆 |
| C、双曲线 | D、抛物线 |
分析:由点A,B分别为双曲线的焦点,再由双曲线的定义可得到∴||CA|-|CB||=2a=6,再由其内切圆结合切线长定理,可求得内切圆圆心的横坐标,与纵坐标无关,所以是两条直线.
解答:解:根据题意:A(-5,0),B(5,0)分别为双曲线的左右焦点.
∴||CA|-|CB||=2a=6
设其内切圆与CA,CB,AB所在的切点分别为E,F,G
由切线长定理可知:|CE|=|CF|,|AE|=|AG|,|BF|=|BG|
∴可得||GA|-|GB||=6
∴xG=3或xG=-3
∴△ABC的内心的轨迹所在图象为两条直线
故选A
∴||CA|-|CB||=2a=6
设其内切圆与CA,CB,AB所在的切点分别为E,F,G
由切线长定理可知:|CE|=|CF|,|AE|=|AG|,|BF|=|BG|
∴可得||GA|-|GB||=6
∴xG=3或xG=-3
∴△ABC的内心的轨迹所在图象为两条直线
故选A
点评:本题主要考查双曲线的定义和三角线的内切圆及圆的切线长定理.

练习册系列答案
相关题目
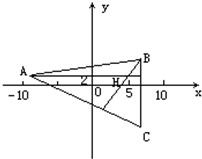 已知△ABC的两个顶点A(-10,2),B(6,4),垂心是H(5,2),求顶点C的坐标.
已知△ABC的两个顶点A(-10,2),B(6,4),垂心是H(5,2),求顶点C的坐标.