题目内容
已知△ABC的两个顶点A,B的坐标分别是(0,-1),(0,1),且AC,BC所在直线的斜率之积等于m(m≠0).
(1)求顶点C的轨迹E的方程,并判断轨迹E为何种圆锥曲线;
(2)当m=-
时,过点F(1,0)的直线l交曲线E于M,N两点,设点N关于x轴的对称点为Q(M,Q不重合) 试问:直线MQ与x轴的交点是否为定点?若是,求出定点,若不是,请说明理由.
(1)求顶点C的轨迹E的方程,并判断轨迹E为何种圆锥曲线;
(2)当m=-
| 1 | 2 |
分析:(1)设出顶点C的坐标,由AC,BC所在直线的斜率之积等于m(m≠0)列式整理得到顶点C的轨迹E的方程,然后分m的不同取值范围判断轨迹E为何种圆锥曲线;
(2)把m=-
代入E得轨迹方程,由题意设出直线l的方程,和椭圆方程联立后利用根与系数关系求出M,N两点的横坐标的和与积,由两点式写出直线MQ的方程,取y=0后求出x,结合根与系数关系可求得x=2,则得到直线MQ与x轴的交点是定点,并求出定点.
(2)把m=-
| 1 |
| 2 |
解答:解:(1)设点C(x,y),由AC,BC所在直线的斜率之积等于m(m≠0),
得:
•
=m,化简得:-mx2+y2=1(x≠0).
当m<-1时,轨迹E表示焦点在y轴上的椭圆,且除去(0,1),(0,-1)两点;
当m=-1时,轨迹E表示以(0,0)为圆心,半径是1的圆,且除去(0,1),(0,-1)两点;
当-1<m<0时,轨迹E表示焦点在x轴上的椭圆,且除去(0,1),(0,-1)两点;
当m>0时,轨迹E表示焦点在y轴上的双曲线,且除去(0,1),(0,-1)两点.
(2)当m=-
时,曲线E的方程为
+y2=1 (x≠0).
由题意可知直线l的斜率存在切不等于0,则可设l:y=k(x-1),
再设M(x1,y1),N(x2,y2),Q(x2,-y2) (x1≠x2).
联立
,得(1+2k2)x2-4k2x+2k2-2=0.
∴x1+x2=
,x1x2=
,
∵M,Q不重合,则x1≠x2,y1≠-y2.
∴MQ所在直线方程为y-y1=
(x-x1),
令y=0,得x=x1+
=x1+
=
=
=2.
∴直线MQ过定点(2,0).
得:
| y-1 |
| x |
| y+1 |
| x |
当m<-1时,轨迹E表示焦点在y轴上的椭圆,且除去(0,1),(0,-1)两点;
当m=-1时,轨迹E表示以(0,0)为圆心,半径是1的圆,且除去(0,1),(0,-1)两点;
当-1<m<0时,轨迹E表示焦点在x轴上的椭圆,且除去(0,1),(0,-1)两点;
当m>0时,轨迹E表示焦点在y轴上的双曲线,且除去(0,1),(0,-1)两点.
(2)当m=-
| 1 |
| 2 |
| x2 |
| 2 |
由题意可知直线l的斜率存在切不等于0,则可设l:y=k(x-1),
再设M(x1,y1),N(x2,y2),Q(x2,-y2) (x1≠x2).
联立
|
∴x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
∵M,Q不重合,则x1≠x2,y1≠-y2.
∴MQ所在直线方程为y-y1=
| y1+y2 |
| x1-x2 |
令y=0,得x=x1+
| y1(x2-x1) |
| y1+y2 |
| k(x1-1)(x2-x1) |
| k(x1+x2-2) |
| 2x1x2-(x1+x2) |
| x1+x2-2 |
=
2•
| ||||
|
∴直线MQ过定点(2,0).
点评:本题考查了与直线有关的动点轨迹方程,考查了椭圆的简单几何性质,考查了分类讨论的数学思想方法,涉及直线和圆锥曲线的关系问题,常采用一元二次方程的根与系数关系求解,从而简化解题过程,此类问题是高考试题中的压轴题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知△ABC的两个顶点A(-5,0),B(5,0),△ABC的第三个顶点在一条双曲线
-
=1(y≠0)上,则△ABC的内心的轨迹所在图象为( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、两条直线 | B、椭圆 |
| C、双曲线 | D、抛物线 |
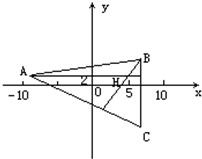 已知△ABC的两个顶点A(-10,2),B(6,4),垂心是H(5,2),求顶点C的坐标.
已知△ABC的两个顶点A(-10,2),B(6,4),垂心是H(5,2),求顶点C的坐标.