题目内容
(1)已知(1-2x)2008=a0+a1x+a2x2+…+a2008x2008(x∈R),求a0+a1+a2+…+a2008的值;
(2)已知(1-2x+3x2)7=a0+a1x+a2x2+…+a13x13+a14x14,求a1+a3+a5+…+a13的值.
(2)已知(1-2x+3x2)7=a0+a1x+a2x2+…+a13x13+a14x14,求a1+a3+a5+…+a13的值.
(1)1 (2)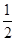 (27-67)
(27-67)
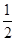 (27-67)
(27-67)解:(1)令x=1,则(1-2x)2008=a0+a1x+a2x2+…+a2008x2008变为(1-2)2008=a0+a1+a2+…+a2008,
∴a0+a1+a2+…+a2008=1.
(2)分别令x=1及x=-1,
可得

两式相减,用上式减下式可得
2(a1+a3+…+a13)=27-67,
∴a1+a3+a5+…+a13=
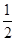 (27-67).
(27-67).
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
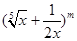 的展开式中第2项为常数项
的展开式中第2项为常数项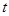 ,其中
,其中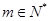 ,且展开式按
,且展开式按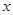 的降幂排列.
的降幂排列.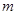 及
及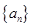 中,
中,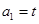 ,
,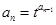 ,
,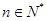 ,求证:
,求证: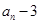 能被4整除.
能被4整除.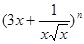 (
(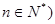 的展开式中含有常数项的最小的
的展开式中含有常数项的最小的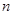 为( )
为( ) ,则x在[0,2π]内的值为________.
,则x在[0,2π]内的值为________.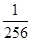 相等,求x的值.
相等,求x的值.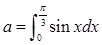 ,则
,则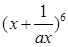 的展开式中的常数项是__________.
的展开式中的常数项是__________.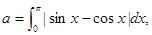 则
则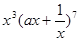 的展开式中的常数项是
的展开式中的常数项是 (用数字作答)
(用数字作答)