题目内容
18.某公司在年终举行的晚会中,为某研发小组的5名成员设置抽奖活动,设定10张券中有一等奖券1张,可获价值500元的奖品;有二等奖券3张,每张可获价值200元的奖品;其余6张设每张可获价值50元的奖品.某成员从此10张券中任抽2张,求:(1)该成员获得价值700元奖品的概率;
(2)该成员获得的奖品总价值x(元)的概率分布列,并求X的数学期望.
分析 (1)某成员从此10张券中任抽2张,基本事件总数为${C}_{10}^{2}$,该成员获得价值700元奖品的情况是抽中一等奖和二等奖,由此能求出该成员获得价值700元奖品的概率.
(2)由题意得X的所有可能取值为100,250,400,550,700,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(1)由题意,得该成员获得价值700元奖品的概率为:
p=$\frac{1×{C}_{3}^{1}}{{C}_{10}^{2}}$=$\frac{1}{15}$.
(2)由题意得X的所有可能取值为100,250,400,550,700,
P(X=100)=$\frac{{C}_{6}^{2}}{{C}_{10}^{2}}$=$\frac{1}{3}$,
P(X=250)=$\frac{{C}_{3}^{1}{C}_{6}^{1}}{{C}_{10}^{2}}$=$\frac{2}{5}$,
P(X=400)=$\frac{{C}_{3}^{2}}{{C}_{10}^{2}}$=$\frac{1}{15}$,
P(X=550)=$\frac{{C}_{6}^{1}}{{C}_{10}^{2}}$=$\frac{2}{15}$,
P(X=700)=$\frac{{C}_{3}^{1}}{{C}_{10}^{2}}$=$\frac{1}{15}$,
∴X的分布列为:
| X | 100 | 250 | 400 | 550 | 700 |
| P | $\frac{1}{3}$ | $\frac{2}{5}$ | $\frac{1}{15}$ | $\frac{2}{15}$ | $\frac{1}{15}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意排列组合知识的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若直线a∥α,直线b∥α,则a与b( )
| A. | 平行 | B. | 异面 | C. | 平行或异面 | D. | 相交、平行或异面 |
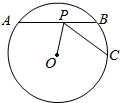 如图,点P为⊙O的弦AB上一点,且AP=9,BP=4,连接OP,作PC⊥OP交圆于C,则PC的长为( )
如图,点P为⊙O的弦AB上一点,且AP=9,BP=4,连接OP,作PC⊥OP交圆于C,则PC的长为( )