题目内容
等差数列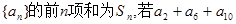 为一个确定的常数,则下列各个前
为一个确定的常数,则下列各个前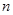 项和中,也为确定的常数的是 ( )
项和中,也为确定的常数的是 ( )
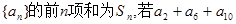 为一个确定的常数,则下列各个前
为一个确定的常数,则下列各个前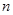 项和中,也为确定的常数的是 ( )
项和中,也为确定的常数的是 ( )| A.S6 | B.S11 | C.S12 | D.S13 |
B
试题分析:根据题意,由于等差数列的等差中项的性质可知,
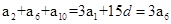 为定值,则根据前n项和与通项公式关系可知,S11 =11
为定值,则根据前n项和与通项公式关系可知,S11 =11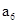 ,因此为常数,故可知选B.
,因此为常数,故可知选B.点评:主要是考查了等差数列的性质的运用,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
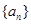 中,
中,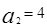 ,其前n项和
,其前n项和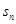 满足
满足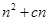
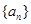 是等差数列,期中
是等差数列,期中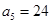 ,
,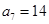
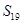
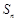 是公差不为0的等差数列
是公差不为0的等差数列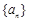 的前
的前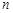 项和,且
项和,且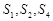 成等比数列,则
成等比数列,则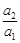 等于
等于
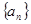 的公差
的公差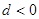 ,且
,且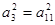 ,则该数列的前
,则该数列的前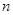 项和取得最大值时,
项和取得最大值时,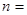
 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称 使得
使得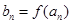 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称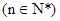 .
.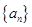 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若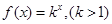 是数列
是数列 的首项为2010,
的首项为2010,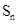 是数列
是数列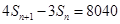 ,证明
,证明 ,
, ,和数列1,
,和数列1,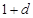 ,
,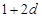 ,(
,( )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.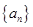 满足:
满足: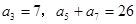 ,
,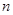 项和为
项和为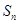 。
。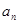 及
及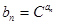 (其中
(其中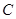 为常数,且
为常数,且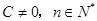 ),求证数列
),求证数列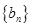 为等比数列。
为等比数列。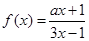 ,且方程
,且方程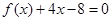 有两个不同的正根,其中一根是另一根的
有两个不同的正根,其中一根是另一根的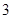 倍,记等差数列
倍,记等差数列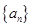 、
、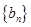 的前
的前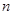 项和分别为
项和分别为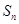 ,
,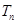 且
且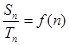 (
(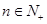 )。
)。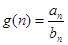 ,求
,求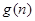 的最大值;
的最大值;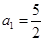 ,数列
,数列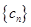 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.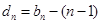 ,
,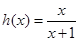 .
. .
.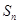 是数列
是数列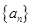 的前
的前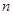 项和,且对任意
项和,且对任意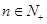 ,有
,有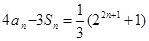 ,
,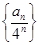 的通项公式;
的通项公式;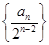 的前
的前 .
.