题目内容
.已知函数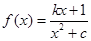 (c>0且c≠1,
(c>0且c≠1, k>0)恰有一个极大值点和一个极小值点,其中一个是
k>0)恰有一个极大值点和一个极小值点,其中一个是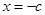 .则函数
.则函数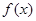 的极大值为 。(用只含k的代数式表示)
的极大值为 。(用只含k的代数式表示)
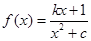 (c>0且c≠1,
(c>0且c≠1, k>0)恰有一个极大值点和一个极小值点,其中一个是
k>0)恰有一个极大值点和一个极小值点,其中一个是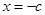 .则函数
.则函数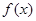 的极大值为 。(用只含k的代数式表示)
的极大值为 。(用只含k的代数式表示)
解:因为函数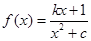 (c>0且c≠1,
(c>0且c≠1, k>0)恰有一个极大值点和一个极小值点,其中一个是
k>0)恰有一个极大值点和一个极小值点,其中一个是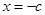 .由题意知f'(-c)=0,即得c2k-2c-ck=0
.由题意知f'(-c)=0,即得c2k-2c-ck=0
∵c≠0,∴k≠0.
由f'(x)=0得-kx2-2x+ck=0,
由韦达定理知另一个极值点为x=1(或x=c-2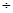 k ).可知极大值为
k ).可知极大值为 。
。
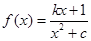 (c>0且c≠1,
(c>0且c≠1, k>0)恰有一个极大值点和一个极小值点,其中一个是
k>0)恰有一个极大值点和一个极小值点,其中一个是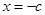 .由题意知f'(-c)=0,即得c2k-2c-ck=0
.由题意知f'(-c)=0,即得c2k-2c-ck=0∵c≠0,∴k≠0.
由f'(x)=0得-kx2-2x+ck=0,
由韦达定理知另一个极值点为x=1(或x=c-2
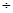 k ).可知极大值为
k ).可知极大值为 。
。
练习册系列答案
相关题目
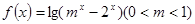
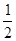 时,求f(x)的定义域
时,求f(x)的定义域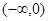 上的单调性并给出证明。
上的单调性并给出证明。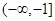 上恒取正值,求m的取值范围。
上恒取正值,求m的取值范围。
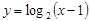
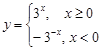
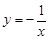
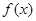 满足
满足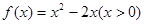 ,则
,则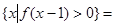
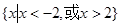
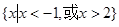
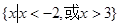
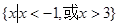
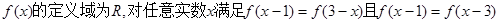 ,当
,当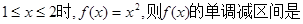 ( )(以下
( )(以下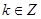 )
)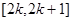
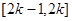
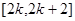
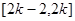
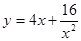
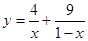 的最小值
的最小值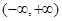 上的偶函数
上的偶函数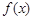 满足:
满足: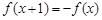 ,且在
,且在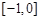 上是增函数,下面关于
上是增函数,下面关于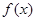 是周期函数;
是周期函数; 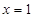 对称;
对称; 上是增函数;
上是增函数; 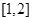 上是减函数;
上是减函数;  .
. 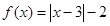 ,
,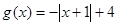 .
.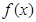 的值不大于
的值不大于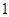 ,求
,求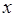 的取值范围;
的取值范围;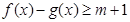 的解集为
的解集为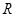 ,求
,求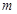 的取值范围.
的取值范围.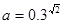 ,
,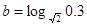 ,
,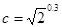 ,a,b,c从小到大排列为
,a,b,c从小到大排列为