题目内容
如图,已知点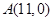 ,函数
,函数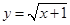 的图象上的动点
的图象上的动点 在
在 轴上的射影为
轴上的射影为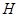 ,且点
,且点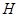 在点
在点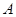 的左侧.设
的左侧.设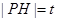 ,
,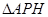 的面积为
的面积为 .
.
(Ⅰ)求函数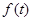 的解析式及
的解析式及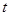 的取值范围;
的取值范围;
(Ⅱ)求函数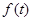 的最大值.
的最大值.
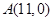 ,函数
,函数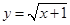 的图象上的动点
的图象上的动点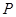 在
在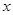 轴上的射影为
轴上的射影为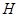 ,且点
,且点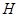 在点
在点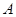 的左侧.设
的左侧.设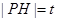 ,
,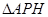 的面积为
的面积为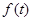 .
.
(Ⅰ)求函数
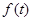 的解析式及
的解析式及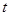 的取值范围;
的取值范围;(Ⅱ)求函数
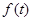 的最大值.
的最大值.(Ⅰ)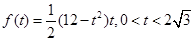 ;(Ⅱ)8.
;(Ⅱ)8.
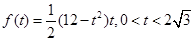 ;(Ⅱ)8.
;(Ⅱ)8.试题分析:(Ⅰ)根据已知条件,需要表示出
 和
和 ,因为
,因为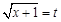 ,所以点
,所以点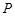 的横坐标为
的横坐标为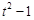 ,
,而
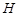 在点
在点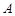 的左侧,所以
的左侧,所以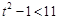 ,即
,即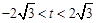 ,由已知
,由已知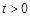 ,所以
,所以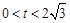 ,则
,则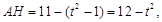 所以
所以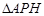 的面积为
的面积为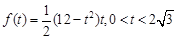 ;(Ⅱ)
;(Ⅱ)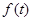 是关于t的三次函数,要求它的最大值,用导数的方法求解,
是关于t的三次函数,要求它的最大值,用导数的方法求解, ,由
,由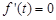 ,得
,得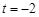 (舍),或
(舍),或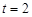 . 根据函数单调性情况,知当
. 根据函数单调性情况,知当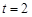 时,函数
时,函数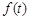 取得最大值8.
取得最大值8.试题解析:(Ⅰ)由已知可得
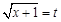 ,所以点
,所以点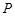 的横坐标为
的横坐标为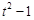 ,
,因为点
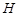 在点
在点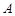 的左侧,所以
的左侧,所以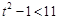 ,即
,即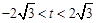 .
.由已知
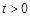 ,所以
,所以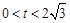 ,
,所以
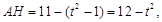
所以
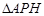 的面积为
的面积为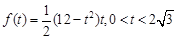 .
.(Ⅱ)

由
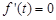 ,得
,得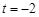 (舍),或
(舍),或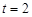 .
.函数
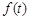 与
与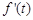 在定义域上的情况如下:
在定义域上的情况如下: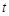 | 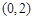 | 2 | 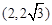 |
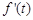 | + | 0 |  |
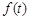 | ↗ | 极大值 | ↘ |
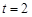 时,函数
时,函数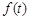 取得最大值8.
取得最大值8.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
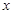 元,
元,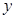 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格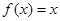 与
与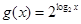
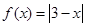 与
与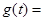
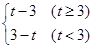
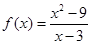 与
与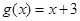
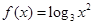 与
与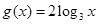
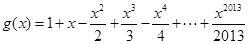 ,则函数
,则函数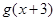 的零点所在的区间为
的零点所在的区间为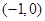
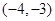
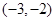 或
或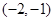
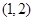
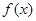 满足
满足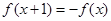 ,且
,且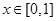 时,
时,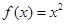 ,若在区间
,若在区间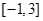 内,函数
内,函数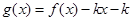 有4个零点,则实数
有4个零点,则实数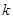 的取值范围是( )
的取值范围是( )
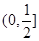


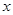 的方程
的方程 有一解,则
有一解,则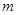 的取值范围为( )
的取值范围为( ) 
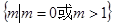
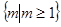
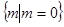
 的零点所在区间是( )
的零点所在区间是( ) )
)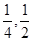 )
)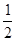 ,1)
,1) 则下列关于函数
则下列关于函数 的零点个数的判断正确的是( )
的零点个数的判断正确的是( ) 时,有3个零点;当
时,有3个零点;当 时,有2个零点
时,有2个零点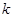 为何值,均有2个零点
为何值,均有2个零点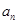 }定义如下:
}定义如下: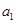 =1,当
=1,当 时,
时,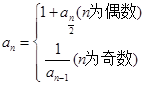 ,若
,若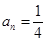 ,则
,则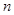 的值等于( )
的值等于( )