题目内容
椐统计从化机械厂生产一种汽车曲轴,由于受生产能力和技术水平的限制,会产生一些次品,该厂生产这种产品的次品率 与日产量x(单位:件)之满足关系
与日产量x(单位:件)之满足关系
 。已知每生产一件合格品可盈利3000元,但每生产一件次品将亏损1500元。
。已知每生产一件合格品可盈利3000元,但每生产一件次品将亏损1500元。
(Ⅰ)判断日产量x超过94时,生产这种产品能否盈利?并说明理由;
(Ⅱ)当日产量x不超过94时,将该厂生产这种产品每天的盈利额y(元)表示成日产量x的函数;为了获得最高日盈利额,日产量应定为多少件?
 与日产量x(单位:件)之满足关系
与日产量x(单位:件)之满足关系 。已知每生产一件合格品可盈利3000元,但每生产一件次品将亏损1500元。
。已知每生产一件合格品可盈利3000元,但每生产一件次品将亏损1500元。(Ⅰ)判断日产量x超过94时,生产这种产品能否盈利?并说明理由;
(Ⅱ)当日产量x不超过94时,将该厂生产这种产品每天的盈利额y(元)表示成日产量x的函数;为了获得最高日盈利额,日产量应定为多少件?
(1)不能盈利(2)84
(Ⅰ)当x>94时,p=  。 ∴每日生产的合格品为
。 ∴每日生产的合格品为 x件,次品为
x件,次品为 x件。
x件。
∴合格品可盈利 元,次品共亏损
元,次品共亏损 元。
元。
∴ ,即日产量超过94件时,盈亏相抵,不能盈利 …………4分
,即日产量超过94件时,盈亏相抵,不能盈利 …………4分
(Ⅱ)当日产量 件时,
件时,
∴每日生产的合格品为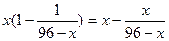 件,次品为
件,次品为 件。
件。
∴ ……7
……7
∴ ……9分
……9分
令 ,可得
,可得 (舍)。…………10分
(舍)。…………10分
∵
∴x=84时,y有最大值。
∴为了获得最高日盈利额,日产量应定为84件。 …………12分
 。 ∴每日生产的合格品为
。 ∴每日生产的合格品为 x件,次品为
x件,次品为 x件。
x件。∴合格品可盈利
 元,次品共亏损
元,次品共亏损 元。
元。∴
 ,即日产量超过94件时,盈亏相抵,不能盈利 …………4分
,即日产量超过94件时,盈亏相抵,不能盈利 …………4分(Ⅱ)当日产量
 件时,
件时,
∴每日生产的合格品为
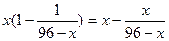 件,次品为
件,次品为 件。
件。∴
 ……7
……7∴
 ……9分
……9分令
 ,可得
,可得 (舍)。…………10分
(舍)。…………10分∵

∴x=84时,y有最大值。
∴为了获得最高日盈利额,日产量应定为84件。 …………12分

练习册系列答案
相关题目
 可近似地用函数
可近似地用函数 来刻画.其中:正整数
来刻画.其中:正整数 表示月份且
表示月份且 ,例如
,例如 时表示1月份;
时表示1月份; 和
和 是正整数;
是正整数; .
. ,
,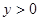 ,函数
,函数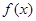 满足
满足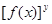 =
=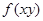 ”的是( )
”的是( ) 1小题满分6分,第2小题满分10分.
1小题满分6分,第2小题满分10分. 米内的圆环面为第
米内的圆环面为第 区、
区、 米的圆环面为第
米的圆环面为第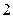 区、……、第
区、……、第 米至
米至 米的圆环面为
米的圆环面为 第
第 区,…,现测得第
区,…,现测得第 、第
、第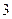 区较第
区较第 山灰总重量最大?
山灰总重量最大?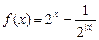 .
.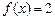 ,求
,求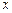 的值;
的值;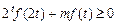 对于
对于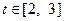 恒成立,求实数
恒成立,求实数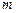 的取值范围.
的取值范围.
 ,那么在区间
,那么在区间 中任取一个值
中任取一个值 ,使
,使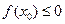 的概率为
的概率为



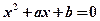 有两个根,一个根在区间
有两个根,一个根在区间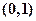 内,另一根在区间
内,另一根在区间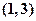 内,记点
内,记点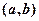 对应的区域为S。那么区域S的面积是_______.
对应的区域为S。那么区域S的面积是_______.