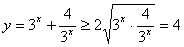题目内容
利用基本不等式求最值,下列运用正确的是( )
分析:利用基本不等式成立的条件分别进行判断即可.
解答:解:A不正确,因为利用基本不等式时没有出现定值.
B不正确,若B正确,当且仅当sinx=
,即sin?2x=4,sinx=2取等号,但sinx∈(0,1),所以等号成立的条件不具备,故不能取等号.
C不正确,因为
和
不一定是正值,当ab<0时,
<0,
<0,不等式不成立..
D.正确.因为3x>0,所以y=3x+
≥2
=4,当且仅当3x=
,即3x=2,x=log32时取等号,满足基本不等式使用的条件.
故选D.
B不正确,若B正确,当且仅当sinx=
| 4 |
| sinx |
C不正确,因为
| b |
| a |
| a |
| b |
| a |
| b |
| b |
| a |
D.正确.因为3x>0,所以y=3x+
| 4 |
| 3x |
3x•
|
| 4 |
| 3x |
故选D.
点评:本题主要考查基本不等式的应用,注意基本不等式成立的三个基本条件:一正,二定,三相等,缺一不可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,求函数
,求函数 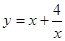 的最小值,并求此时x的值.
的最小值,并求此时x的值.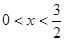 ,求函数
,求函数 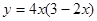 的最大值.
的最大值.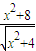 的最值时,我们可以将
的最值时,我们可以将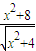 化成
化成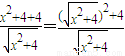 ,再将分式分解成
,再将分式分解成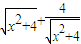 ,然后利用基本不等式求最值;借此,计算使得
,然后利用基本不等式求最值;借此,计算使得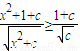 对一切实数x都成立的正实数c的范围是 .
对一切实数x都成立的正实数c的范围是 .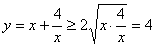 B.
B.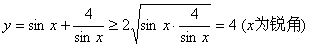
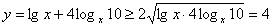 D.
D.