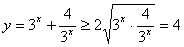题目内容
(12分)利用基本不等式求最值:
(1)若 ,求函数
,求函数 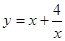 的最小值,并求此时x的值.
的最小值,并求此时x的值.
(2)设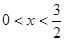 ,求函数
,求函数 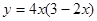 的最大值.
的最大值.
【答案】
(1)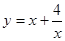 在x =
2时取得最小值4 .(2)
在x =
2时取得最小值4 .(2)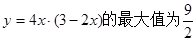 。
。
【解析】(I)根据基本不等式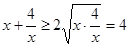 , 可直接求出y的最小值,并求出此时的x值.
, 可直接求出y的最小值,并求出此时的x值.
(2)因为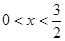 , 所以3-2x>0,
, 所以3-2x>0,
所以 ,
据此得到y的最大值.
,
据此得到y的最大值.
(1)当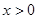 时,
时,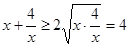 ,所以当且仅当
,所以当且仅当 ,即x=2时取等号.
,即x=2时取等号.
因此,函数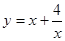 在x = 2时取得最小值4
.
在x = 2时取得最小值4
.
(2)由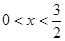 得,
得, ,所以
,所以
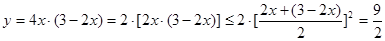 ,
,
当且仅当2x=3-2x,即x = 时取等号.因此,函数
时取等号.因此,函数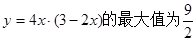

练习册系列答案
相关题目
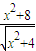 的最值时,我们可以将
的最值时,我们可以将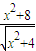 化成
化成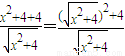 ,再将分式分解成
,再将分式分解成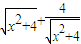 ,然后利用基本不等式求最值;借此,计算使得
,然后利用基本不等式求最值;借此,计算使得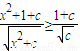 对一切实数x都成立的正实数c的范围是 .
对一切实数x都成立的正实数c的范围是 .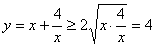 B.
B.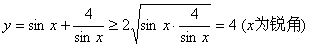
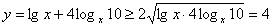 D.
D.