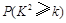题目内容
计算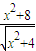 的最值时,我们可以将
的最值时,我们可以将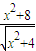 化成
化成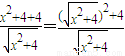 ,再将分式分解成
,再将分式分解成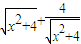 ,然后利用基本不等式求最值;借此,计算使得
,然后利用基本不等式求最值;借此,计算使得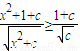 对一切实数x都成立的正实数c的范围是 .
对一切实数x都成立的正实数c的范围是 .
【答案】分析:由题意,将不等式的左边进行分离为 ,这是积为定值的两个式子的和.在x2+c=1时,即x2=-c+1≥0,它的最小值为2.此时c∈(0,1].接下来讨论当c>1时和0<c≤1的两种情况下不等式左边的最小值,再解这个最小值大于或等于
,这是积为定值的两个式子的和.在x2+c=1时,即x2=-c+1≥0,它的最小值为2.此时c∈(0,1].接下来讨论当c>1时和0<c≤1的两种情况下不等式左边的最小值,再解这个最小值大于或等于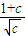 ,最后可得正实数c的范围.
,最后可得正实数c的范围.
解答:解:根据已知条件给出的模型,得到启发:
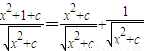
=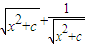
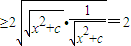
当且仅当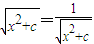 时等号成立,此时x2+c=1
时等号成立,此时x2+c=1
①当c>1时,x2+c>1,以上不等式的等号不能成立,
所以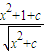 的最小值应该是x=0时的值,即
的最小值应该是x=0时的值,即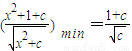
因此不等式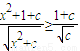 对一实数x都成立,符合题意.
对一实数x都成立,符合题意.
②当0<c≤1时,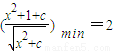
若要使得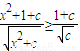 对一切实数x都成立
对一切实数x都成立
必须有:2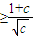 成立,可得
成立,可得
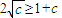 ⇒
⇒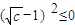 ⇒c=1
⇒c=1
综上所述,c∈[1,+∞)
故答案为:[1,+∞)
点评:本题以不等式恒成立和函数的最值为载体,考查了类比推理的方法,属于中档题.归纳推理与类比推理都属于合情推理,是数学发现的常用推理过程.
 ,这是积为定值的两个式子的和.在x2+c=1时,即x2=-c+1≥0,它的最小值为2.此时c∈(0,1].接下来讨论当c>1时和0<c≤1的两种情况下不等式左边的最小值,再解这个最小值大于或等于
,这是积为定值的两个式子的和.在x2+c=1时,即x2=-c+1≥0,它的最小值为2.此时c∈(0,1].接下来讨论当c>1时和0<c≤1的两种情况下不等式左边的最小值,再解这个最小值大于或等于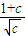 ,最后可得正实数c的范围.
,最后可得正实数c的范围.解答:解:根据已知条件给出的模型,得到启发:
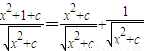
=
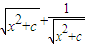
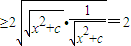
当且仅当
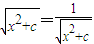 时等号成立,此时x2+c=1
时等号成立,此时x2+c=1①当c>1时,x2+c>1,以上不等式的等号不能成立,
所以
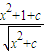 的最小值应该是x=0时的值,即
的最小值应该是x=0时的值,即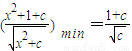
因此不等式
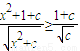 对一实数x都成立,符合题意.
对一实数x都成立,符合题意.②当0<c≤1时,
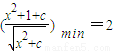
若要使得
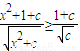 对一切实数x都成立
对一切实数x都成立必须有:2
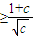 成立,可得
成立,可得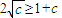 ⇒
⇒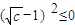 ⇒c=1
⇒c=1综上所述,c∈[1,+∞)
故答案为:[1,+∞)
点评:本题以不等式恒成立和函数的最值为载体,考查了类比推理的方法,属于中档题.归纳推理与类比推理都属于合情推理,是数学发现的常用推理过程.

练习册系列答案
相关题目
经过对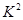 的统计量的研究,得到了若干个临界值,当
的统计量的研究,得到了若干个临界值,当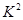 的观测值
的观测值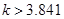 时,我们( )
时,我们( )
|
|
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
A. 在错误的概率不超过0.05的前提下可认为A与B有关
B. 在错误的概率不超过0.05的前提下可认为A与B无关
C. 在错误的概率不超过0.01的前提下可认为A与B有关
D.没有充分理由说明事件A与B有关