题目内容
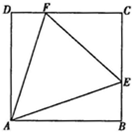
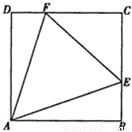
在福建省第14届运动会开幕式上,主会场中央有一块边长为a米的正方形地面全彩LED显示屏如图所示,点E、F分虽为BC、CD边上异于点C的动点,现在顶点A处有视角∠EAF设置为45°的摄像机,正录制形如△ECF的移动区域内表演的某个文艺节目,设DF=x米,BE=y米.(Ⅰ)试将y表示为x的函数;
(Ⅱ)求证:△ECF周长p为定值;
(Ⅲ)求△ECF面积S的最大值.
【答案】分析:(Ⅰ)利用∠EAF=45°及和角三角函数可构建x,y之间的关系,从而得出x,y之间的函数关系式;
(Ⅱ)关键是表达出△ECF的周长,结合(Ⅰ)将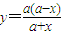 代入化简可证;
代入化简可证;
(Ⅲ)首先可以得到S=xy,因此要求面积的最大值,关键是求xy的最大值,利用(Ⅰ),结合基本不等式可以求出面积的最大值.
解答:解:(Ⅰ)因为∠EAF=45°,DF=x米,BE=y米,
所以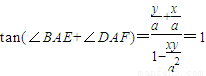 ,
,
所以a(x+y)=a2-xy,所以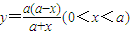 ;
;
(Ⅱ)△ECF的周长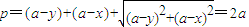 ,
,
所以△ECF的周长p为定值;
(Ⅲ) ,
,
由(Ⅰ)知a(x+y)=a2-xy,得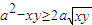 ,解得
,解得 ,
,
当且仅当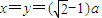 时,
时,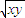 取到最大值
取到最大值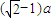 ,所以
,所以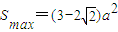 ,
,
所以△ECF面积S的最大值为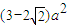 平方米.
平方米.
点评:本题主要考查函数、不等式等基础知识;考查运算求解能力以及应用数学知识分析和解决实际问题的能力;考查应用意识.
(Ⅱ)关键是表达出△ECF的周长,结合(Ⅰ)将
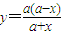 代入化简可证;
代入化简可证;(Ⅲ)首先可以得到S=xy,因此要求面积的最大值,关键是求xy的最大值,利用(Ⅰ),结合基本不等式可以求出面积的最大值.
解答:解:(Ⅰ)因为∠EAF=45°,DF=x米,BE=y米,
所以
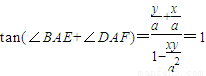 ,
,所以a(x+y)=a2-xy,所以
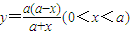 ;
;(Ⅱ)△ECF的周长
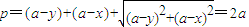 ,
,所以△ECF的周长p为定值;
(Ⅲ)
 ,
,由(Ⅰ)知a(x+y)=a2-xy,得
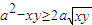 ,解得
,解得 ,
,当且仅当
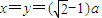 时,
时,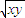 取到最大值
取到最大值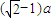 ,所以
,所以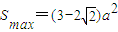 ,
,所以△ECF面积S的最大值为
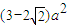 平方米.
平方米.点评:本题主要考查函数、不等式等基础知识;考查运算求解能力以及应用数学知识分析和解决实际问题的能力;考查应用意识.

练习册系列答案
相关题目