题目内容
f(x)=x2-2x-3,求f(3)、f(5)、f(-5)并计算f(3)+f(5)+f(-5).设计一个解决该问题的算法,并画出流程图.
思路分析:本题考查简单的求函数值的顺序结构的程序框图的作法.这是简单的求函数值问题,我们直接代入即可求得函数值.
解:算法如下:
第一步,输入x=3;第二步,输出y1=x2-2x-3;第三步,输入x=-5;
第四步,输出y2=x2-2x-3;第五步,输入x=5;第六步,输出y3=x2-2x-3;第七步,输出y=y1+y2+y3.
算法流程图如图1-1-10.
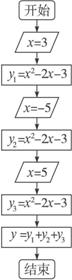
图1-1-10
方法归纳 本题不是很特殊,但说明了一般函数(非分段函数)的函数值的求法就是一个简单的顺序结构.但是要注意类似于拓展变式中关于迭代的函数思想的掌握.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
已知函数f(x)=
(x≠0),则以下结论正确的是( )
| x2+2 |
| x |
A、f(x)在定义域内,最大值是2
| ||||
B、f(x)在定义域内,最大值是-2
| ||||
C、f(x)在(-∞,0)上,最大值是-2
| ||||
D、f(x)在(0,+∞)上,最大值是2
|