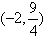题目内容
设f(x)=
|
分析：本题是解一个分段函数不等式，故要分类求解，最后再将所得的两段上符合条件的范围并起来．
解答：解：∵f(x)=
，f（t）＞2
∴当x≥0时，x2-2x-1＞2，解得x＞3，或x＜-1，故得x＞3
当x＜0时，-2x+6＞2，解得x＜2，故得x＜0
综上知实数t的取值范围是（-∞，0）∪（3，+∞）
故答案为：（-∞，0）∪（3，+∞）．
|
∴当x≥0时，x2-2x-1＞2，解得x＞3，或x＜-1，故得x＞3
当x＜0时，-2x+6＞2，解得x＜2，故得x＜0
综上知实数t的取值范围是（-∞，0）∪（3，+∞）
故答案为：（-∞，0）∪（3，+∞）．
点评：本题考查其它不等式的解法，解题的关键是根据函数的特点，对不等式分类求解，正确解出不等式的解集也很关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
)
，+∞)
,+∞)
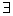x0∈(0，+∞)使得f(x0)≥g(x0)，则实数m的取值范围是
B. 
C. 
D. 