题目内容
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
由散点图可知,销售量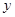 与价格
与价格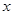 之间有较好的线性相关关系,其线性回归直线方程是;
之间有较好的线性相关关系,其线性回归直线方程是;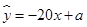
(1)求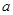 的值;
的值;
(2)预计在今后的销售中,销量与单价仍然服从线性回归直线方程中的关系,且该产品的成本是每件4元,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入一成本)
(1)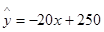 ;(2) 当单价定为8.25元时,工厂可获得最大利润.
;(2) 当单价定为8.25元时,工厂可获得最大利润.
解析试题分析:(1)分别求出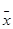 ,
,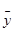 ,代入回归直线方程
,代入回归直线方程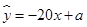 中,可求出参数
中,可求出参数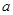 ,进而求出回归直线方程;(2) 设工厂获得的利润为
,进而求出回归直线方程;(2) 设工厂获得的利润为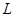 元,依题意得:
元,依题意得: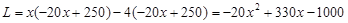 ,由此能求出当单价定为8.25元时,工厂可获得最大利润.
,由此能求出当单价定为8.25元时,工厂可获得最大利润.
试题解析:(1)由于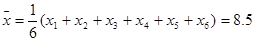 ,
,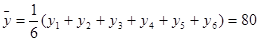 .
.
所以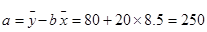 .即所求回归方程为
.即所求回归方程为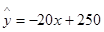 .
.
(2)设工厂获得的利润为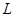 元,依题意得:
元,依题意得: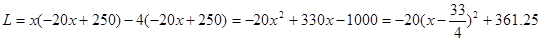 .
.
当且仅当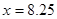 时,
时,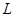 取得最大值.故当单价定为8.25元时,工厂可获得最大利润.
取得最大值.故当单价定为8.25元时,工厂可获得最大利润.
考点:回归分析的初步应用.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(1)用分层抽样的方法在喜欢打蓝球的学生中抽6人,其中男生抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女生的概率.
某公司销售A、B、C三款手机,每款手机都有经济型和豪华型两种型号,据统计12月份共销售1000部手机(具体销售情况见下表)
| | A款手机 | B款手机 | C款手机 |
| 经济型 | 200 | x | y |
| 豪华型 | 150 | 160 | z |
已知在销售1000部手机中,经济型B款手机销售的频率是0.21.
(1)现用分层抽样的方法在A、B、C三款手机中抽取50部,求应在C款手机中抽取多少部?
(2)若y
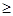 136,z
136,z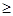 133,求C款手机中经济型比豪华型多的概率.
133,求C款手机中经济型比豪华型多的概率. (本小题满分12分)
海关对同时从 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测
| 地区 |  |  |  |
| 数量 | 50 | 150 | 100 |
(1)求这6件样品中来自
 各地区商品的数量;
各地区商品的数量;(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“ ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |  |  |  |  |  |  |  |  |  |  |
空气质量指数( ) ) |  |  |  |  |  |  |  |  |  |  |
“ ” ” 小时平均浓度( 小时平均浓度( ) ) |  |  |  |  |  |  |  |  |  |  |
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件
 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘ ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率;
发生的概率;(3)在上表数据中,在表示空气质量优良的日期中,随机抽取
 天,记
天,记 为“
为“ ”
” 小时平均浓度不超过
小时平均浓度不超过 的天数,求
的天数,求 的分布列和数学期望.
的分布列和数学期望. 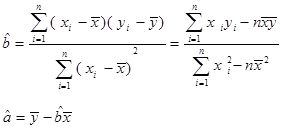

 与价格
与价格 之间有较好的线性相关关系,其线性回归直线方程是;
之间有较好的线性相关关系,其线性回归直线方程是;
 的值;
的值;