题目内容
某公司销售A、B、C三款手机,每款手机都有经济型和豪华型两种型号,据统计12月份共销售1000部手机(具体销售情况见下表)
| | A款手机 | B款手机 | C款手机 |
| 经济型 | 200 | x | y |
| 豪华型 | 150 | 160 | z |
已知在销售1000部手机中,经济型B款手机销售的频率是0.21.
(1)现用分层抽样的方法在A、B、C三款手机中抽取50部,求应在C款手机中抽取多少部?
(2)若y
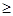 136,z
136,z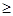 133,求C款手机中经济型比豪华型多的概率.
133,求C款手机中经济型比豪华型多的概率.
(1)14;(2)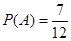 .
.
解析试题分析:(1)由已知,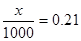 ,可得
,可得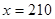 .从而求得手机C的总数为280部.根据分层抽样的性质即可得到在C款手机中抽取手机数.
.从而求得手机C的总数为280部.根据分层抽样的性质即可得到在C款手机中抽取手机数.
(2)设“C款手机中经济型比豪华型多”为事件A,C款手机中经济型、豪华型手机数记为(y,z),满足事件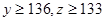 的基本事件有12个,其中事件A包含的基本事件有7个.所以C款手机中经济型比豪华型多的概率为.
的基本事件有12个,其中事件A包含的基本事件有7个.所以C款手机中经济型比豪华型多的概率为.
试题解析:(1) 因为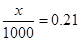 ,所以
,所以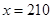 2分
2分
所以手机 的总数为:
的总数为: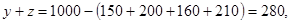 3分
3分
现用分层抽样的方法在在 、
、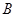 、
、 三款手机中抽取
三款手机中抽取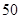 部手机,应在
部手机,应在 款手机中抽取手机数为:
款手机中抽取手机数为: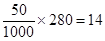 (部) 5分
(部) 5分
(2)设“ 款手机中经济型比豪华型多”为事件
款手机中经济型比豪华型多”为事件 ,
, 款手机中经济型、豪华型手机数记为
款手机中经济型、豪华型手机数记为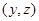 ,因为
,因为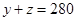 ,
,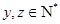 ,满足事件
,满足事件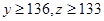 的基本事件有:
的基本事件有: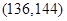 ,
,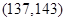 ,
,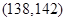 ,
,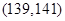 ,
,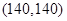 ,
,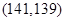 ,
, ,
,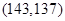 ,
,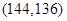 ,
,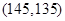 ,
,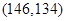 ,
,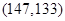 共
共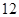 个
个
事件 包含的基本事件为
包含的基本事件为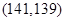 ,
, ,
,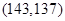 ,
,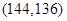 ,
,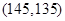 ,
,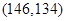 ,
,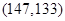 共7个,所以
共7个,所以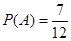
即 款手机中经济型比豪华型多的概率为
款手机中经济型比豪华型多的概率为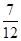 12分
12分
考点:1.古典概型的概率计算;2.分层抽样.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
为了检验“喜欢玩手机游戏与认为作业多”是否有关系,某班主任对班级的30名学生进行了调查,得到一个2×2列联表:
| | 认为作业多 | 认为作业不多 | 合计 |
| 喜欢玩手机游戏 | 18 | 2 | |
| 不喜欢玩手机游戏 | | 6 | |
| 合计 | | | 30 |
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);
(Ⅱ)能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系?
(Ⅲ)若从不喜欢玩手机游戏的人中随机抽取3人,则至少2人认为作业不多的概率是多少?
假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
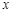 | 2 | 3 | 4 | 5 | 6 |
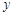 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
某校在高二年级开设了 ,
,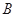 ,
, 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从
三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从 ,
,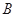 ,
, 三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
| 兴趣小组 | 小组人数 | 抽取人数 |
 | 12 | 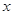 |
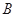 | 36 | 3 |
 | 48 | 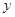 |
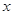 ,
,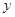 的值;
的值;(2)若从
 ,
,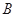 两个兴趣小组所抽取的人中选2人作专题发言,求这2人都来自兴趣小组
两个兴趣小组所抽取的人中选2人作专题发言,求这2人都来自兴趣小组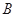 的概率.
的概率. 某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示.已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16.
| | 第一批次 | 第二批次 | 第三批次 |
| 女教职工 | 196 | x | y |
| 男教职工 | 204 | 156 | z |
(1)求x的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?
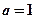 是函数
是函数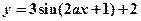 的周期为
的周期为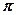 的充要条件;②老师在班级50名学生中,依次抽取学号为5,10,15,20,25,30,35,40,45,50的学生进行作业检查,这种抽样方法是系统抽样;③若“存在
的充要条件;②老师在班级50名学生中,依次抽取学号为5,10,15,20,25,30,35,40,45,50的学生进行作业检查,这种抽样方法是系统抽样;③若“存在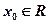 ,使得
,使得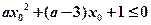 ”是假命题,则
”是假命题,则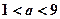 ;④某人向一个圆内投镖,则镖扎到该圆的内接正三角形区域内的概率为
;④某人向一个圆内投镖,则镖扎到该圆的内接正三角形区域内的概率为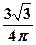 .其中正确的是 .
.其中正确的是 .
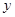 与价格
与价格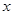 之间有较好的线性相关关系,其线性回归直线方程是;
之间有较好的线性相关关系,其线性回归直线方程是;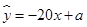
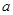 的值;
的值;

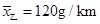 .
.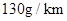 的概率是多少?
的概率是多少? 的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.