题目内容
下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“ ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |  |  |  |  |  |  |  |  |  |  |
空气质量指数( ) ) |  |  |  |  |  |  |  |  |  |  |
“ ” ” 小时平均浓度( 小时平均浓度( ) ) |  |  |  |  |  |  |  |  |  |  |
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件
 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘ ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率;
发生的概率;(3)在上表数据中,在表示空气质量优良的日期中,随机抽取
 天,记
天,记 为“
为“ ”
” 小时平均浓度不超过
小时平均浓度不超过 的天数,求
的天数,求 的分布列和数学期望.
的分布列和数学期望.
(1)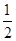 ;(2)
;(2)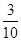 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)首先根据表格中的数据找出空气质量优良的天数,然后利用古典概型的概率计算公式即可求出当月某日空气质量优良的概率;(2)先确定(1)中所选的 天中
天中 的
的 小时平均浓度不超过
小时平均浓度不超过 对应的天数,利用排列组合思想与古典概型计算相应事件的概率;(3)先确定随机变量
对应的天数,利用排列组合思想与古典概型计算相应事件的概率;(3)先确定随机变量 的可能取值,然后利用超几何分布的特点求出随机变量
的可能取值,然后利用超几何分布的特点求出随机变量 在对应取值下的概率,列出分布列计算其数学期望即可.
在对应取值下的概率,列出分布列计算其数学期望即可.
(1)由上表数据知, 天中空气质量指数(
天中空气质量指数( )小于
)小于 的日期有:
的日期有: 、
、 、
、 、
、 、
、 共
共 天,
天,
故可估计该市当月某日空气质量优良的概率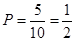 ;
;
(2)由(1)知 天中表示空气质量为优良的天数为
天中表示空气质量为优良的天数为 ,当天“
,当天“ 的
的 小时平均浓度不超过
小时平均浓度不超过 有编号为
有编号为 、
、 、
、 ,共
,共 天,
天,
故事件 发生的概率
发生的概率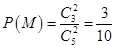 ;
;
(3)由(1)知, 的可能取值为
的可能取值为 、
、 、
、 ,
,
且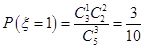 ,
,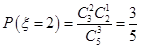 ,
,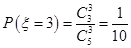 ,
,
故 的分布列为:
的分布列为:




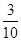
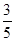
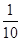
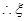 的数学期望
的数学期望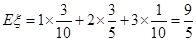 .
.
考点:1.古典概型;2.超几何分步;3.离散型随机分布列与数学期望

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
某种产品的广告费用支出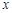 (万元)与销售额
(万元)与销售额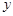 (万元)之间有如下的对应数据:
(万元)之间有如下的对应数据:
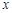 | 2 | 4 | 5 | 6 | 8 |
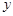 | 30 | 40 | 60 | 50 | 70 |
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为9万元时,销售收入
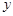 的值.
的值.参考公式:回归直线的方程
 ,其中
,其中 .
. 某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x/℃ | 10 | 11 | 13 | 12 | 8 |
| 发芽数y /颗 | 23 | 25 | 30 | 26 | 16 |
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程
 =bx+a;
=bx+a;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?

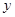 与价格
与价格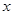 之间有较好的线性相关关系,其线性回归直线方程是;
之间有较好的线性相关关系,其线性回归直线方程是;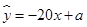
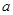 的值;
的值;
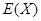 及方差
及方差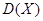 .
. 元/张
元/张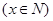 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少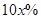 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少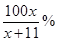 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?

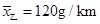 .
.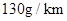 的概率是多少?
的概率是多少? 的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.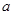 表示.
表示.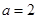 时,分别从甲,乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
时,分别从甲,乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
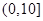 ,第2组
,第2组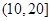 ,第3组
,第3组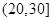 ,第4组
,第4组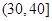 ,第5组
,第5组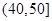 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示. 
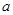 的值
的值