Question

【题目】已知椭圆C：1（a＞b＞0）过A（2，0），B（0，1）两点.

（1）求椭圆C的方程和离心率的大小；

（2）设M，N是y轴上不同的两点，若两点的纵坐标互为倒数，直线AM与椭圆C的另一个交点为P，直线AN与椭圆C的另一个交点为Q，判断直线PQ与x轴的位置关系，并证明你的结论.

Answer 1

【答案】（1）；离心率（2）直线PQ与x轴平行；证明见解析

【解析】

（1）依题意得a＝2，b＝1，写出椭圆C的方程，求解离心率的大小即可.

（2）设M，N坐标为（0，m），（0，n），则，m≠0，n≠0，由A（2，0），M（0，m）得直线AM的方程为，联立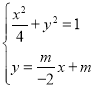，求出P的纵坐标，Q纵坐标，然后推出结果.

解法二：设直线AM的方程为x＝ty+2（t≠0），直线AN的方程为x＝sy+2（s≠0）令x＝0得tyM＝﹣2，M坐标为，同理N坐标为，推出yP＝yQ≠0，直线PQ与x轴平行.

解法三：设直线AM的方程为y＝k1（x﹣2），k1≠0，直线AN的方程为y＝k2（x﹣2），k2≠0，令x＝0得M坐标为（0，﹣2k1），同理N坐标为（0，﹣2k2），得到4k1k2＝1，代入椭圆方程求出P的纵坐标，Q的纵坐标，即可得到结果.

（1）依题意得a＝2，b＝1，所以椭圆C的方程为，，

离心率的大小.

（2）解法一、因为M，N是y轴上不同的两点，两点的纵坐标互为倒数，

设M，N坐标为（0，m），（0，n），则，m≠0，n≠0

由A（2，0），M（0，m）得直线AM的方程为，，

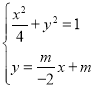整理得（m2+1）y2﹣2my＝0或（m2+1）x2﹣4m2x+4m2﹣4＝0，

得交点P的纵坐标为，

同理交点Q的纵坐标为，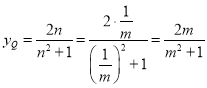

所以yP＝yQ≠0，直线PQ与x轴平行.

解法二：

设直线AM的方程为x＝ty+2（t≠0），直线AN的方程为x＝sy+2（s≠0），

令x＝0得tyM＝﹣2，M坐标为，同理N坐标为，

因为M，N是y轴上不同的两点，两点的纵坐标互为倒数，所以st＝4，，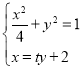

整理得（t2+4）y2+4ty＝0或（t2+4）x2﹣16x+16﹣4t2＝0，

得交点P的纵坐标为，

同理得，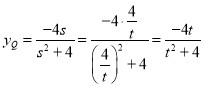

所以yP＝yQ≠0，直线PQ与x轴平行.

解法三：

设直线AM的方程为y＝k1（x﹣2），k1≠0，直线AN的方程为y＝k2（x﹣2），k2≠0

令x＝0得M坐标为（0，﹣2k1），同理N坐标为（0，﹣2k2），

因为M，N是y轴上不同的两点，两点的纵坐标互为倒数，所以4k1k2＝1，

代入椭圆方程得，，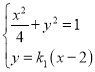

或所以，

得交点P的纵坐标为，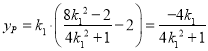

同理得，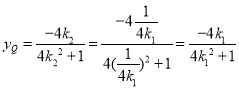

所以yP＝yQ≠0，直线PQ与x轴平行.