题目内容
17.已知区域D由不等式组$\left\{\begin{array}{l}{0≤x≤\sqrt{2}}\\{y≤2}\\{x≤\sqrt{2}y}\end{array}\right.$给定,若点M(x,y)为D上的动点,点A($\sqrt{2}$,1),则$\overrightarrow{OM}$•$\overrightarrow{OA}$的最大值为4.分析 首先画出可行域,z=$\overrightarrow{OM}$•$\overrightarrow{OA}$代入坐标变为z=$\sqrt{2}$x+y,即y=-$\sqrt{2}$x+z,z表示斜率为$-\sqrt{2}$的直线在y轴上的截距,故求z的最大值,即求y=-$\sqrt{2}$x+z与可行域有公共点时在y轴上的截距的最大值
解答 解:由不等式组$\left\{\begin{array}{l}{0≤x≤\sqrt{2}}\\{y≤2}\\{x≤\sqrt{2}y}\end{array}\right.$给定的区域D如图所示: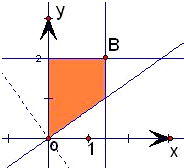
z=$\overrightarrow{OM}$•$\overrightarrow{OA}$=$\sqrt{2}$x+y,即y=-$\sqrt{2}$x+z
首先做出直线l0:y=-$\sqrt{2}$x,将l0平行移动,当经过B点时在y轴上的截距最大,从而z最大.
因为B( $\sqrt{2}$,2),故z的最大值为4;
故答案为:4.
点评 本题考查线性规划、向量的坐标表示、平面向量数量积的运算等基础知识,考查运算求解能力,考查数形结合思想.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
2.已知复数z1=2+i,z2=1+2i,则z=$\frac{z_2}{z_1}$在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |