题目内容
 (2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.
(2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.(1)求证:AG上平面BCG;
(2)求直线BE与平面ACG所成角的正弦值.
分析:(1)设B点在平面AGC内的射影为H,则H在CG上,由BH⊥平面AGC,知BH⊥AG,BC⊥AB,又平面ABCD⊥平面ABEF,则BC⊥平面ABEF,可得BC⊥AG,根据线面垂直的判定定理可知AG⊥平面BGC;
(2)延长AG、BE交于K,连HK,因为BH⊥面ACG,所以∠KHB即为直线BE与平面ACG所成角,求出BH、BK,即可求得结论.
(2)延长AG、BE交于K,连HK,因为BH⊥面ACG,所以∠KHB即为直线BE与平面ACG所成角,求出BH、BK,即可求得结论.
解答: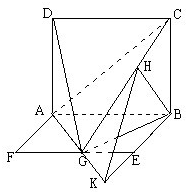 (1)证明:设B点在平面AGC内的射影为H,则H在CG上,
(1)证明:设B点在平面AGC内的射影为H,则H在CG上,
由BH⊥平面AGC,知BH⊥AG,
∵ABCD为正方形,∴BC⊥AB,又平面ABCD⊥平面ABEF,
∴BC⊥平面ABEF,又AG?平面ABEF,
∴BC⊥AG,又BH、BC?平面BCG,
∴AG⊥平面BCG;
(2)解:延长AG、BE交于K,连HK,
因为BH⊥面ACG,所以∠KHB即为直线BE与平面ACG所成角.
由(1)知,AG⊥平面BCG,故AG⊥BG,
∵AF=BE=
AB,BG=
AB,
∴BH=
=
=
AB.
∴sin∠KHB=
=
.
∴直线BE与平面ACG所成角为arcsin
.
 (1)证明:设B点在平面AGC内的射影为H,则H在CG上,
(1)证明:设B点在平面AGC内的射影为H,则H在CG上,由BH⊥平面AGC,知BH⊥AG,
∵ABCD为正方形,∴BC⊥AB,又平面ABCD⊥平面ABEF,
∴BC⊥平面ABEF,又AG?平面ABEF,
∴BC⊥AG,又BH、BC?平面BCG,
∴AG⊥平面BCG;
(2)解:延长AG、BE交于K,连HK,
因为BH⊥面ACG,所以∠KHB即为直线BE与平面ACG所成角.
由(1)知,AG⊥平面BCG,故AG⊥BG,
∵AF=BE=
| 1 |
| 2 |
| ||
| 2 |
∴BH=
| BC•BG |
| CG |
AB•
| ||||
|
| ||
| 3 |
∴sin∠KHB=
| BH |
| BK |
| ||
| 3 |
∴直线BE与平面ACG所成角为arcsin
| ||
| 3 |
点评:本题主要考查了直线与平面垂直的判定,以及平面与平面垂直的性质和二面角的度量,同时考查了化归与转化的数学思想方法,以及空间想象能力、运算求解能力和推理论证能力,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
 (2010•河东区一模)设集合S={x|x2-2x<3},T={x|1-x2<0},则如图中阴影表示的集合为( )
(2010•河东区一模)设集合S={x|x2-2x<3},T={x|1-x2<0},则如图中阴影表示的集合为( )