题目内容
设函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R,a>0)其中,f(0)=3,f′(x)是f(x)的导函数.(Ⅰ)若f′(-1)=f′(3)=-36,f′(5)=0,求函数f(x)的解析式;
(Ⅱ)若c=-6,函数f(x)的两个极值点为x1,x2满足-1<x1<1<x2<2.设λ=a2+b2-6a+2b+10,试求实数λ的取值范围.
【答案】分析:(1)由于f(0)=3,则d=3,求出导数后分别代入-1,3,5,得到三个关系式,解出a,b,c,即可得到函数f(x)的解析式;
(2)根据题意知f(x)=ax3+bx2-6x+3,由于函数f(x)的两个极值点为x1,x2满足-1<x1<1<x2<2.则得到a与b满足不等式组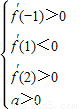 即得到点(a,b)的可行区域,又由于λ=a2+b2-6a+2b+10=(a-3)2+(b+1)2,依据其几何意义,即可求出λ的取值范围.
即得到点(a,b)的可行区域,又由于λ=a2+b2-6a+2b+10=(a-3)2+(b+1)2,依据其几何意义,即可求出λ的取值范围.
解答: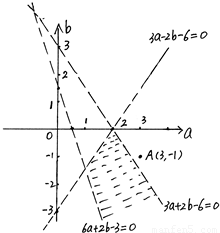 (Ⅰ)由于f(0)=3,则d=3,
(Ⅰ)由于f(0)=3,则d=3,
而f'(x)=3ax2+2bx+c…(1分)
由f′(-1)=f′(3)=-36,f′(5)=0知
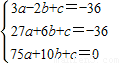 ….(2分)
….(2分)
解得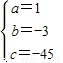 …(4分)
…(4分)
故f(x)=x3-3x2-45x+3即为所求.…(5分)
(Ⅱ) 据题意,函数f(x)=ax3+bx2-6x+3,则f′(x)=3ax2+2bx-6
又x1,x2是方程f′(x)=0的两根,且-1<x1<1<x2<2,a>0.
则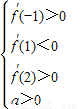 即
即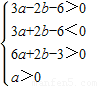 …(7分)
…(7分)
则点(a,b)的可行区域如图…(10分)
由于λ=a2+b2-6a+2b+10=(a-3)2+(b+1)2,
则λ的几何意义为点P(a,b)与点A(3,-1)的距离的平方.….….(11分)
观察图形知点,A到直线3a+2b-6=0的距离的平方d2为λ的最小值
而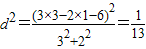
故λ的取值范围是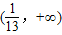 …..(13分).
…..(13分).
点评:此题考查导数的概念及应用以及线性规划的问题,是一道中档题.
(2)根据题意知f(x)=ax3+bx2-6x+3,由于函数f(x)的两个极值点为x1,x2满足-1<x1<1<x2<2.则得到a与b满足不等式组
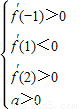 即得到点(a,b)的可行区域,又由于λ=a2+b2-6a+2b+10=(a-3)2+(b+1)2,依据其几何意义,即可求出λ的取值范围.
即得到点(a,b)的可行区域,又由于λ=a2+b2-6a+2b+10=(a-3)2+(b+1)2,依据其几何意义,即可求出λ的取值范围.解答:
 (Ⅰ)由于f(0)=3,则d=3,
(Ⅰ)由于f(0)=3,则d=3,而f'(x)=3ax2+2bx+c…(1分)
由f′(-1)=f′(3)=-36,f′(5)=0知
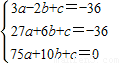 ….(2分)
….(2分)解得
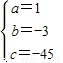 …(4分)
…(4分)故f(x)=x3-3x2-45x+3即为所求.…(5分)
(Ⅱ) 据题意,函数f(x)=ax3+bx2-6x+3,则f′(x)=3ax2+2bx-6
又x1,x2是方程f′(x)=0的两根,且-1<x1<1<x2<2,a>0.
则
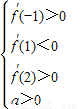 即
即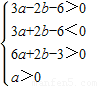 …(7分)
…(7分)则点(a,b)的可行区域如图…(10分)
由于λ=a2+b2-6a+2b+10=(a-3)2+(b+1)2,
则λ的几何意义为点P(a,b)与点A(3,-1)的距离的平方.….….(11分)
观察图形知点,A到直线3a+2b-6=0的距离的平方d2为λ的最小值
而
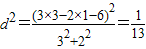
故λ的取值范围是
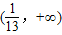 …..(13分).
…..(13分).点评:此题考查导数的概念及应用以及线性规划的问题,是一道中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |