题目内容
4.设f(x)=lg($\frac{2}{1-x}$+a)(-1<x<1)是奇函数,则f(-$\frac{9}{11}$)=-1.分析 根据奇函数的性质即可求出a的值,得到函数的解析式,将x=-$\frac{9}{11}$代入可得答案.
解答 解:∵f(x)=lg($\frac{2}{1-x}$+a)是奇函数,
∴f(0)=0,
即f(0)=lg(2+a)=0,
解得a=-1,
故f(x)=lg($\frac{2}{1-x}$-1),
故f(-$\frac{9}{11}$)=-1,
故答案为:-1
点评 本题主要考查了对数函数的图象和性质,属于基础题

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
15.设a=${log}_{\frac{1}{5}}$3,b=($\frac{1}{3}$)0.4,c=4${\;}^{\frac{1}{3}}$,则( )
| A. | c>b>a | B. | c>a>b | C. | b>a>c | D. | a>b>c |
14.动直线x=m(m>0)与函数f(x)=2x+$\frac{1}{x}$,g(x)=x-$\frac{1}{x}$-lnx分别交于点A,B,则|AB|的最小值为( )
| A. | 3+ln2 | B. | 2 | C. | $\frac{7}{2}$-ln2 | D. | 3 |
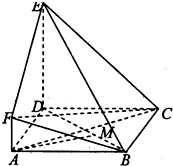 如图,ABCD是边长为3的正方形,AF∥DE,DE=3AF.
如图,ABCD是边长为3的正方形,AF∥DE,DE=3AF.