题目内容
16.函数y=$\frac{1-tanx}{1+tanx}$的单调递减区间是(kπ-$\frac{π}{2}$,kπ-$\frac{π}{4}$),(kπ-$\frac{π}{4}$,kπ+$\frac{π}{2}$).y=sin2(x-$\frac{π}{6}$)减区间(kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$).分析 先求出函数的导数,解关于导函数的不等式,从而求出函数的递减区间.
解答 解:(1)∵y=$\frac{1-tanx}{1+tanx}$=$\frac{cosx-sinx}{cosx+sinx}$,
∴y′=$\frac{(cosx-sinx)′(cosx+sinx)-(cosx-sinx)(cosx+sinx)′}{{(cosx+sinx)}^{2}}$
=-$\frac{2}{{(cosx+sinx)}^{2}}$<0,
∴函数在定义域内单调递减,
∵kπ-$\frac{π}{2}$<x<kπ+$\frac{π}{2}$,且1+tanx≠0,解得;x≠kπ-$\frac{π}{4}$,
∴函数y=$\frac{1-tanx}{1+tanx}$的单调递减区间是(kπ-$\frac{π}{2}$,kπ-$\frac{π}{4}$),(kπ-$\frac{π}{4}$,kπ+$\frac{π}{2}$);
(2)∵y=sin2(x-$\frac{π}{6}$)=$\frac{1-cos(2x-\frac{π}{3})}{2}$,
∴y′=sin(2x-$\frac{π}{3}$),
令y′<0,解得:kπ-$\frac{π}{3}$<x<kπ+$\frac{π}{6}$,
∴函数y=sin2(x-$\frac{π}{6}$)的减区间是(kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$),
故答案为:(kπ-$\frac{π}{2}$,kπ-$\frac{π}{4}$),(kπ-$\frac{π}{4}$,kπ+$\frac{π}{2}$);(kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$).
点评 本题考查了函数的单调性问题,考查导数的应用,三角函数问题,是一道中档题.

| A. | (-∞,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (-∞,1)∪(1,+∞) | D. | (-∞,0)∪(0,1)∪(1,+∞) |
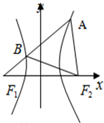 如图,F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( )
如图,F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( )| A. | 4 | B. | $\sqrt{7}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |