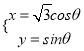题目内容
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(Ⅰ)当![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() , 若
, 若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,当
的“类对称点”,当![]() 时,试问
时,试问![]() 是否存在“类对称点”,若存在,请求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请求出一个“类对称点”的横坐标;若不存在,请说明理由.
【答案】(Ⅰ)函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间为
,单调递减区间为![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时,函数
时,函数![]() 存在“类对称点”.
存在“类对称点”.
【解析】试题分析:(Ⅰ)求出函数的导数,结合![]() 的范围求出函数的单调区间即可;(Ⅱ)法一:
的范围求出函数的单调区间即可;(Ⅱ)法一: ![]() 时,求出
时,求出![]() 的导数,得到切线方程根据新定义问题等价于当
的导数,得到切线方程根据新定义问题等价于当![]() 时,
时, ![]() ,结合函数的单调性求出即可;法二:猜想
,结合函数的单调性求出即可;法二:猜想![]() 存在“类对称点”,其中一个“类对称点”的横坐标为
存在“类对称点”,其中一个“类对称点”的横坐标为![]() ,然后加以证明即可.
,然后加以证明即可.
试题解析:(Ⅰ)解 函数![]() 的定义域为
的定义域为![]() ,因为
,因为![]()
所以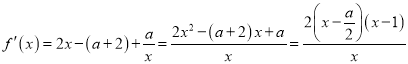 , 因
, 因![]() ,
, ![]()
由![]() ,即
,即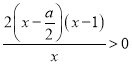 得
得![]() 或
或![]() , 由
, 由![]() 得
得![]() ;
;
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(Ⅱ)解法一:当![]() 时,
时, ![]()
所以在点![]() 处的切线方程为
处的切线方程为![]()
令![]()
则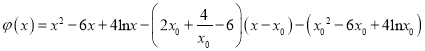
易知![]() ;
;
又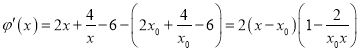 =0
=0
则![]()
当![]() 时,
时, ![]() ,令
,令![]() ,则
,则![]() ,所以函数
,所以函数![]() 在
在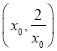 上单调递减,所以当
上单调递减,所以当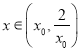 时,
时, ![]() ,从而有
,从而有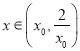 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]() 在
在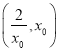 上单调递减,所以当
上单调递减,所以当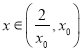 时,
时, ![]() ,从而有
,从而有 时,
时, ![]() ;
;
所以当![]() 时,函数
时,函数![]() 不存在“类对称点”。 ……11分
不存在“类对称点”。 ……11分
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
当![]() 时,
时, ![]() ,
, ![]()
当![]() 时,
时, ![]() ,
, ![]()
故![]() 恒成立
恒成立
所以当![]() 时,函数
时,函数![]() 存在“类对称点”.
存在“类对称点”.
(Ⅱ)解法二
当![]() 时,
时, ![]()
所以在点![]() 处的切线方程为
处的切线方程为![]()
若函数![]() 存在“类对称点”
存在“类对称点” ![]()
则等价当![]() 时,
时, ![]() ,当
,当![]() 时
时![]() 恒成立
恒成立
当![]() 时
时![]() 恒成立,
恒成立,
等价于![]() 恒成立
恒成立
即![]()
令![]()
而![]()
![]()
要使![]() 在
在![]() 恒成立,只要
恒成立,只要![]() 在
在![]() 单调递增即可
单调递增即可
所以![]() ,即
,即![]() 当
当![]() 时
时![]() 恒成立,同理可得
恒成立,同理可得![]() ,
,
所以![]()
所以函数![]() 存在“类对称点”,其中一个“类对称点”横坐标为
存在“类对称点”,其中一个“类对称点”横坐标为![]() .
.

练习册系列答案
相关题目