题目内容
某中学举办“上海世博会”知识宣传活动,现场的“抽卡有奖游戏”特别引人注目,游戏规则是:盒子中装有8张形状大小相同的精美卡片,卡片上分别印有“世博会吉祥物海宝”或“世博会会徽”,要求4人一组参加游戏,参加游戏的4人从盒子中轮流抽取卡片,一次抽2张,抽取后不放回,直到4人中某人一次抽到2张“世博会吉祥物海宝”卡才能获奖,当某人获奖或者盒中卡片抽完时游戏终止.(Ⅰ)游戏开始之前,一位高中生问:“盒子中有几张‘世博会会徽’卡?”主持人说:“若从盒中任抽2张卡片不都是‘世博会会徽’卡的概率为
| 25 | 28 |
(Ⅱ)在(Ⅰ)的条件下,甲、乙、丙、丁4人参加游戏,约定甲、乙、丙、丁依次抽取.用随机变量ξ表示游戏终止时总共抽取的次数(注意,一次抽取的是两张卡片),求ξ的分布列和数学期望.
分析:(Ⅰ)根据若从盒中任抽2张卡片不都是世博会会徽卡的概率,写出2张卡片不都是世博会会徽的对立事件的概率,写出2张卡片不都是世博会会徽的对立事件的概率,根据对立事件的概率公式得到概率,列出方程,得到结果.
(II)ξ表示游戏终止时,所有人共抽取卡片的次数,得到变量的可能取值,结合变量对应的事件,写出分布列,利用期望公式得到变量的期望.
(II)ξ表示游戏终止时,所有人共抽取卡片的次数,得到变量的可能取值,结合变量对应的事件,写出分布列,利用期望公式得到变量的期望.
解答:解:(Ⅰ)设盒子中有“会徽卡”n张,
∵若从盒中任抽2张卡片不都是‘世博会会徽’卡的概率为
依题意有1-
=
,
解得n=3,
即盒中有“会徽卡”3张.
(Ⅱ)ξ表示游戏终止时,所有人共抽取卡片的次数,
∴ξ的所有可能取值为1,2,3,4,
P(ξ=1)=
=
;
P(ξ=2)=
•
+
•
=
;P(ξ=3)=
•
•
+
•
•
+
•
•
=
;P(ξ=4)=
•
•
•
=
,
∴随机变量ξ的分布列为:
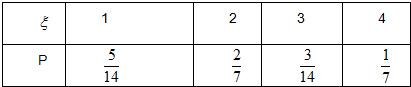
∴ξ的数学期望为Eξ=1×
+2×
+3×
+4×
=
.
∵若从盒中任抽2张卡片不都是‘世博会会徽’卡的概率为
| 25 |
| 28 |
依题意有1-
| ||
|
| 25 |
| 28 |
解得n=3,
即盒中有“会徽卡”3张.
(Ⅱ)ξ表示游戏终止时,所有人共抽取卡片的次数,
∴ξ的所有可能取值为1,2,3,4,
P(ξ=1)=
| ||
|
| 5 |
| 14 |
P(ξ=2)=
| ||
|
| ||
|
| ||||
|
| ||
|
| 2 |
| 7 |
| ||
|
| ||||
|
| ||
|
| ||||
|
| ||
|
| ||
|
| ||||
|
| ||||
|
| ||
|
| 3 |
| 14 |
| ||||
|
| ||||
|
| ||||
|
| ||
|
| 1 |
| 7 |
∴随机变量ξ的分布列为:

∴ξ的数学期望为Eξ=1×
| 5 |
| 14 |
| 2 |
| 7 |
| 3 |
| 14 |
| 1 |
| 7 |
| 15 |
| 7 |
点评:本题考查离散型随机变量的分布列和期望,考查对立事件的概率,考查互斥事件的概率,是一个综合题,注意解题的格式.

练习册系列答案
相关题目
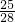 ”请你回答有几张“世博会会徽”卡呢?
”请你回答有几张“世博会会徽”卡呢? ”请你回答有几张“世博会会徽”卡呢?
”请你回答有几张“世博会会徽”卡呢? ”请你回答有几张“世博会会徽”卡呢?
”请你回答有几张“世博会会徽”卡呢?