题目内容
某中学举办“上海世博会”知识宣传活动，现场的“抽卡有奖游戏”特别引人注目，游戏规则是：盒子中装有8张形状大小相同的精美卡片，卡片上分别印有“世博会吉祥物海宝”或“世博会会徽”，要求两人一组参加游戏，参加游戏的两人从盒子中轮流抽取卡片，一次抽1张，抽取后不放回，直到两人中的一人抽到“世博会会徽”卡得奖才终止游戏．（Ⅰ）游戏开始之前，一位高中生问：“盒子中有几张‘世博会会徽’卡？”主持人说：“若从盒中任抽2张卡片不都是‘世博会会徽’卡的概率为
| 25 | 28 |
（Ⅱ）在（Ⅰ）的条件下，甲、乙两人参加游戏，双方约定甲先抽取乙后抽取，求甲获奖的概率．
分析：（Ⅰ）因为已知抽2张卡片不都是‘世博会会徽’卡的概率为
，求盒子中有几张“世博会会徽”卡．故可设盒子中有“会徽卡”n张，然后求出其反面：抽取2张都是“世博会会徽”卡的概率，然后用1减去它等于
，解出n即可．
（Ⅱ）求甲获奖的概率，由题意甲最多可能摸三次，故分为甲第一次抽取就中奖，甲第二次抽取才中奖，甲第三次抽取才中奖三种情况．分别求出它们的概率相加即可得到甲获奖的概率．
| 25 |
| 28 |
| 25 |
| 28 |
（Ⅱ）求甲获奖的概率，由题意甲最多可能摸三次，故分为甲第一次抽取就中奖，甲第二次抽取才中奖，甲第三次抽取才中奖三种情况．分别求出它们的概率相加即可得到甲获奖的概率．
解答：（Ⅰ）解：设盒子中有“会徽卡”n张，
依题意有，1-
=
，
解得n=3．
即盒中有“会徽卡”3张．
（Ⅱ）解：由（1）知，甲最多可能摸三次，
若甲第一次抽取就中奖，则P1=
=
；
若甲第二次抽取才中奖，则P2=
•
•
=
；
若甲第三次抽取才中奖，则P3=
•
•
•
•
=
，
∴甲获奖的概率为P=P1+P2+P3=
+
+
=
．
依题意有，1-
| ||
|
| 25 |
| 28 |
解得n=3．
即盒中有“会徽卡”3张．
（Ⅱ）解：由（1）知，甲最多可能摸三次，
若甲第一次抽取就中奖，则P1=
| ||
|
| 3 |
| 8 |
若甲第二次抽取才中奖，则P2=
| ||
|
| ||
|
| ||
|
| 5 |
| 28 |
若甲第三次抽取才中奖，则P3=
| ||
|
| ||
|
| ||
|
| ||
|
| ||
|
| 3 |
| 56 |
∴甲获奖的概率为P=P1+P2+P3=
| 3 |
| 8 |
| 5 |
| 28 |
| 3 |
| 56 |
| 17 |
| 28 |
点评：此题主要考查等可能事件的概率的求法，对于此类实际应用问题，体现了“新课程”的要求，虽考查知识点少，但有一定的技巧性，属于中档题目．
练习册系列答案
相关题目
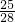”请你回答有几张“世博会会徽”卡呢？
”请你回答有几张“世博会会徽”卡呢？
”请你回答有几张“世博会会徽”卡呢？