题目内容
6．已知函数f（x）=$\frac{{x}^{2}}{x-2}$（x∈R且x≠2）．求f（x）的单调区间．分析 先求出函数的导数，解关于导函数的不等式，从而求出函数的单调区间．
解答 解：f′（x）=$\frac{2x（x-2）{+x}^{2}}{{（x-2）}^{2}}$=$\frac{{3x}^{2}-4x}{{（x-2）}^{2}}$=$\frac{x（3x-4）}{{（x-2）}^{2}}$，
令f′（x）＞0，解得：x＞$\frac{4}{3}$或x＜0，
令f′（x）＜0，解得：0＜x＜$\frac{4}{3}$，
∴函数f（x）在（-∞，0），（$\frac{4}{3}$，2），（2，+∞）递增，
在（0，$\frac{4}{3}$）递减．
点评 本题考查了函数的单调性，导数的应用，是一道基础题．
练习册系列答案
相关题目
14．已知函数f（x）=sinx+x2013，令f1（x）=f′（x），f2（x）=f1′（x），f3（x）=f2′（x），…，fn+1（x）=fn′（x），则f2014（x）=（ ）
| A． | -sinx | B． | -sinx+x | C． | cosx | D． | cosx+x |
11．
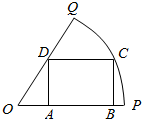如图所示，扇形OPQ的半径为2，圆心角为$\frac{π}{3}$，C是扇形弧上的动点，四边形ABCD是扇形的内接矩形，则SABCD的最大值是（ ）
如图所示，扇形OPQ的半径为2，圆心角为$\frac{π}{3}$，C是扇形弧上的动点，四边形ABCD是扇形的内接矩形，则SABCD的最大值是（ ）| A． | $\frac{2\sqrt{3}}{3}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | $\frac{2}{3}$ |