题目内容
| |||||||||||
中，侧棱PA⊥底面ABCD，AD∥BC，∠ABC＝
，
，
．
的大小．解析：
(1) |
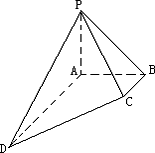
解：如图，在四棱锥
∵BC∥AD，从而点D到平面PBC间的距离等于点A 到平面PBC的距离． ∵∠ABC＝ 又PA⊥底面ABCD，∴PA⊥BC， ∴BC⊥平面PAB，………………2分 ∴平面PAB⊥平面PBC，交线为PB， 过A作AE⊥PB，垂足为E，则AE⊥平面PBC， ∴AE的长等于点D到平面PBC的距离． 而 即点D到平面PBC的距离为 解法二：如图，以A为原点，分别以AD、AB、AP为x轴、y轴、z轴建立空间直角坐标系．
依题意 ∴ ∴
∴ 设平面PBC的一个法向量为
则点D到平面PBC的距离等于 |
(2) |
方法一：∵PA⊥底面ABCD，∴平面PAD⊥底面ABCD， 引CM⊥AD于M，MN⊥PD于N，则CM⊥平面PAD， ∴MN是CN在平面PAD上的射影，
由三垂线定理可知CN⊥PD， ∴∠CNM是二面角 依题意 ∴ 可知
∴二面角 方法二：∵AB⊥PA，AB⊥AD， ∴AB⊥底面PDA，∴平面PDA的一个法向量为 设平面PDC的一个法向量为 ∵ 令 ∵二面角 ∴二面角 |
中，
，∴AB⊥BC，
，∴
．………………5分
．………………6分
，
，
，
．则
，
，
，
，
，
，
．
，则
令
，得
，
的平面角．…………9分
，∴
，
，
．………………12分
．
，
，∴
，得
，∴
．
．………………12分
| |||||||||||
有两个不相等的实数根且必有一个根属于
；
的根为m，且
成等差数列，设函数f(x)的图象的对称轴方程为x＝x0，求证：x0＜m2．
| |||||||||||||||
，求证：
；
使得
，试证对于任意
，f(x)＞0总成立；