题目内容
设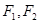
分别是椭圆
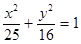的左、右焦点，
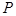为椭圆上任一点，点
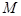的坐标为
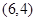，则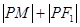
的最大值为 ．
【答案】
15
【解析】本试题主要考查了椭圆的性质的运用，结合三点共线求解最值。
由题意F2（3，0），|MF2|=5，由椭圆的定义可得，|PM|+|PF1|=2a+|PM|-|PF2|=10+|PM|-|PF2|≤10+|MF2|=15，当且仅当P，F2，M三点共线时取等号，故答案为：15
解决该试题的关键是将问题转换为PM|+|PF1|=2a+|PM|-|PF2|，结合对称性可知，只有当P，F2，M三点共线时满足题意。
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
分别是椭圆
的左、右焦点，P是其右准线上纵坐标为
（
为半焦距）的点，且
，则椭圆的离心率是
B. 
C. 
D. 
的焦点在
轴上
的焦距为1，求椭圆
分别是椭圆的左、右焦点，
为椭圆
交
轴与点
，并且
，证明：当
变化时，点
在某定直线上。
分别是椭圆
的左、右焦点．
是该椭圆上的一点，且
，求
的面积；
是该椭圆上的一个动点，求
的最大值和最小值；
的直线
与椭圆交于不同的两点
，且
为锐角（其中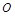
为坐标原点），求直线
的取值范围．
分别是椭圆的
左，右焦点。
是第一象限内该椭圆上的一点，且
，求点
的直线与椭圆交于不同的两点
，且
为锐角（其中O为坐标原点），求直线
的斜率
的取值范围。
分别是椭圆
的左、右焦点，过
斜率为1的直线
与
相交于
两点，且
成等差数列。
满足
，求