题目内容
已知函数 ,
, (其中
(其中 ).
).
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)若函数 在区间
在区间 内有两个零点,求正实数a的取值范围;(Ⅲ)求证:当
内有两个零点,求正实数a的取值范围;(Ⅲ)求证:当 时,
时, .(说明:e是自然对数的底数,e=2.71828…)
.(说明:e是自然对数的底数,e=2.71828…)
(Ⅰ)极小值为 ,无极大值(Ⅱ)
,无极大值(Ⅱ) (Ⅲ)问题等价于
(Ⅲ)问题等价于 .由(Ⅰ)知
.由(Ⅰ)知 的最小值为
的最小值为 .设
.设 ,
, 得
得 在
在 上单调递增,在
上单调递增,在 上单调递减.∴
上单调递减.∴ ,
,
∵
 =
= ,∴
,∴ ,∴
,∴ ,故当
,故当 时,
时,
解析试题分析:(Ⅰ) ,
,
∴ (
( ,
, ),
),
由 ,得
,得 ,由
,由 ,得
,得 ,
,
故函数 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
所以函数 的极小值为
的极小值为 ,无极大值. 4分
,无极大值. 4分
(Ⅱ)函数 ,
,
则
 ,
,
令 ,∵
,∵ ,解得
,解得 ,或
,或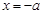 (舍去),
(舍去),
当 时,
时, ,
, 在
在 上单调递减;
上单调递减;
当 时,
时, ,
, 在
在 上单调递增.
上单调递增.
函数 在区间
在区间 内有两个零点,
内有两个零点,
只需 即
即 ∴
∴
故实数a的取值范围是 . 9分
. 9分
(Ⅲ)问题等价于 .由(Ⅰ)知
.由(Ⅰ)知 的最小值为
的最小值为 .
.
设 ,
, 得
得 在
在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
∴ ,
,
∵
 =
= ,
,
∴ ,∴
,∴ ,故当
,故当 时,
时, . 14分
. 14分
考点:函数极值最值
点评:求函数极值最值都需要首先找到函数的单调区间,第二问将函数存在零点转化为最值边界值的范围,第三问将不等式恒成立问题转化为求函数最值问题,这两种转化是函数综合题中经常考到的

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 是幂函数且在
是幂函数且在 上为减函数,函数
上为减函数,函数 在区间
在区间 上的最大值为2,试求实数
上的最大值为2,试求实数 的值。
的值。 (1-a)x2-3ax+1,a>0.
(1-a)x2-3ax+1,a>0.
 的奇偶性;
的奇偶性; 上是增函数还是减函数?证明你的结论.
上是增函数还是减函数?证明你的结论.

 的单调递增区间;
的单调递增区间; 的定义域为
的定义域为 ,值域为[2,5],求m的值。
,值域为[2,5],求m的值。 在
在 与
与 时都取得极值
时都取得极值 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。