题目内容
设数列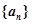 的前
的前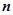 项和为
项和为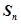 ,且满足
,且满足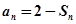
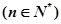 .
.
(Ⅰ)求出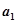 ,
,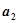 ,
,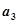 ,
,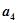 的值;
的值;
(Ⅱ)猜想数列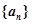 的通项公式,并证明.
的通项公式,并证明.
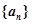 的前
的前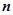 项和为
项和为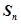 ,且满足
,且满足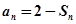
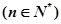 .
.(Ⅰ)求出
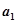 ,
,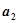 ,
,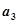 ,
,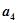 的值;
的值;(Ⅱ)猜想数列
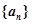 的通项公式,并证明.
的通项公式,并证明.(Ⅰ)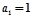 ;
;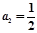 ;
; ;
;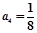 . (Ⅱ)
. (Ⅱ)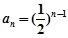
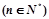 .
.
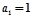 ;
;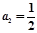 ;
; ;
;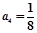 . (Ⅱ)
. (Ⅱ)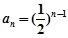
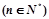 .
. (Ⅰ)代入所给式子即可求出数列的前几项;(Ⅱ)根据第一问的结论猜想出 数列的通项公式,然后按照数学归纳法的步骤证明即可。
(Ⅰ)由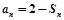 ,得
,得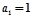 ;
;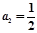 ;
; ;
;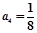 . ………4分
. ………4分
(Ⅱ)猜想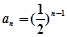
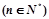 . 证明:
. 证明: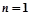 时,
时, ,
,
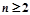 时,
时,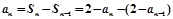 ,即
,即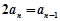 ,∴
,∴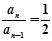
∴ 是以
是以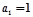 为首项,
为首项,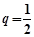 为公比的等比数列,∴
为公比的等比数列,∴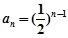
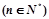 .
.
(Ⅰ)由
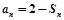 ,得
,得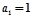 ;
;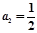 ;
; ;
;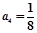 . ………4分
. ………4分(Ⅱ)猜想
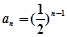
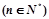 . 证明:
. 证明: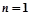 时,
时, ,
,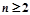 时,
时,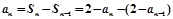 ,即
,即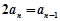 ,∴
,∴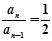
∴
 是以
是以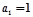 为首项,
为首项,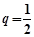 为公比的等比数列,∴
为公比的等比数列,∴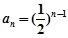
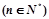 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
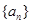 的通项公式为
的通项公式为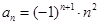 ,其前
,其前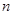 项和为
项和为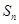 ,
,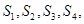 并猜想
并猜想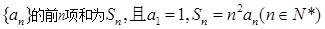 。
。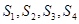 的值;
的值;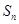 的表达式并用数学归纳法证明。
的表达式并用数学归纳法证明。 }的前n项和为Sn,且S3 =6,则5a1+a7,的值为
}的前n项和为Sn,且S3 =6,则5a1+a7,的值为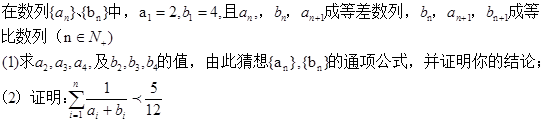
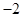 的等差数列
的等差数列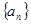 的前
的前 项和为
项和为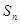 ,且
,且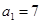 ,则使
,则使 成立的最小的自然数
成立的最小的自然数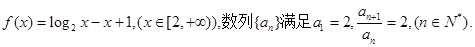
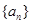 的通项公式
的通项公式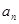 ;
;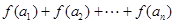 ;
;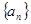 是各项正的等比数列,且
是各项正的等比数列,且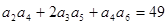 ,则
,则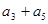 =
=