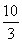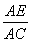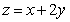题目内容
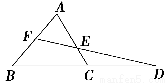
如图所示,D为△ABC中BC边上的一点,∠CAD=∠B,若AD=6,AB=10,BD=8,求CD的长.

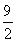
【解析】
解 在△ABD中,AD=6,AB=10,BD=8,满足AB2=AD2+BD2,∴∠ADB=90°,
即AD⊥BC.
又∵∠CAD=∠B,且∠C+∠CAD=90°.
∴∠C+∠B=90°,即∠BAC=90°,
故在Rt△BAC中,AD⊥BC,
由射影定理知AD2=BD·CD,即62=8·CD,∴CD=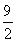 .
.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目