题目内容
设函数f（x）=ax2+8x+3（a＜0），对于给定的负实数a，有一个最大正数l（a），使得x∈[0，l（a）]时，不等式|f（x）|≤5都成立．
（1）当a=-2时，求l（a）的值；
（2）a为何值时，l（a）最大，并求出这个最大值，证明你的结论．
分析：由题意（1）由于a=-2，代入函数f（x）=ax2+8x+3（a＜0），使得f（x）的解析式具体，画出图形即可；
（2）由题意及二次函数为开口向下的要使x∈[0，l（a）]时，不等式|f（x）|≤5都成立，利用分类讨论的思想可以求解．
（2）由题意及二次函数为开口向下的要使x∈[0，l（a）]时，不等式|f（x）|≤5都成立，利用分类讨论的思想可以求解．
解答：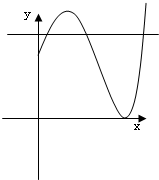
解：（1）当a=-2，f（x）=-2x2+8x+3最大值11，
令|f（x）|=5只须考虑-2x2+8x+3=5
得x=2±
．如图，l（a）=2-
．
（2）f（x）=ax2+8x+3，
∵a＜0，对称轴x=-
＞0，f（x）的最大值
=
，
当
＞5即a＞-8时，取x2+8x+3=5得x=
．
如图l(a)=
=
＜
，
当
≤5即a≤-8时，
取-（ax2+8x+3）=5得x=
，
取l(a)=
=
≤
=
（当a=-8时取等号）
∴当a=-8时，l（a）最大，最大值是
．
解：（1）当a=-2，f（x）=-2x2+8x+3最大值11，令|f（x）|=5只须考虑-2x2+8x+3=5
得x=2±
| 3 |
| 3 |
（2）f（x）=ax2+8x+3，
∵a＜0，对称轴x=-
| 4 |
| a |
| 4×3•a-64 |
| 4a |
| 3a-16 |
| a |
当
| 3a-16 |
| a |
-4±
| ||
| a |
如图l(a)=
-4+
| ||
| a |
| 2 | ||
|
| 1 |
| 2 |
当
| 3a-16 |
| a |
取-（ax2+8x+3）=5得x=
-4±
| ||
| a |
取l(a)=
-4-
| ||
| a |
| 8 | ||
|
| 8 | ||
|
| ||
| 2 |
（当a=-8时取等号）
∴当a=-8时，l（a）最大，最大值是
| ||
| 2 |
点评：此题考查了二次函数在闭区间上的最值，还考查了分类讨论的思想及无理不等式的求解．
练习册系列答案
相关题目
设函数f（x）=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |