题目内容
在任意△
ABC中,求证:a(sinB-sinC)+b(sinC-sinA)+c(sinA-sinB)=0.
答案:略
解析:
解析:
|
证明:由正弦定理知 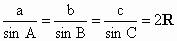 ,a=2RsinA,b=2RsinB,c=2RsinC. ,a=2RsinA,b=2RsinB,c=2RsinC.
故左边 =2RsinA(sinB-sinC)+2RsinB(sinC-sinA)+2RsinC(sinA-sinB)=2R[sinAsinB -sinAsinC+sinBsinC-sinAsinB+sinAsinC-sinBsinC]=2R ×0=0=右边,证毕. |

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
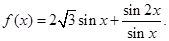
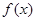 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。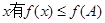 ,且b=1,c=2,求a的值。
,且b=1,c=2,求a的值。
 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。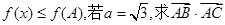 的最大值.
的最大值.