题目内容
已知函数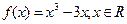 ,又
,又 由
由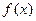 向右平移1个单位,向上平移2个单位得到.
向右平移1个单位,向上平移2个单位得到.
(I)判断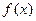 的奇偶性,并求出
的奇偶性,并求出 的极大值与极小值之和.
的极大值与极小值之和.
(II)过点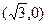 且方向向量为
且方向向量为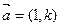 的直线与
的直线与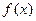 的图像相切,求实数
的图像相切,求实数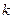 的值.
的值.
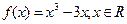 ,又
,又 由
由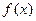 向右平移1个单位,向上平移2个单位得到.
向右平移1个单位,向上平移2个单位得到.(I)判断
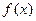 的奇偶性,并求出
的奇偶性,并求出 的极大值与极小值之和.
的极大值与极小值之和.(II)过点
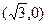 且方向向量为
且方向向量为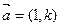 的直线与
的直线与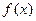 的图像相切,求实数
的图像相切,求实数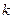 的值.
的值.(I) 是奇函数
是奇函数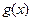 极大+
极大+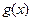 极小=4. (II)
极小=4. (II)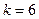 或
或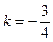 .
.
 是奇函数
是奇函数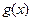 极大+
极大+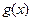 极小=4. (II)
极小=4. (II)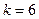 或
或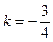 .
. (I)由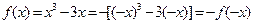 , ――――――――(2分)
, ――――――――(2分)
又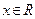 ,故
,故 是奇函数. ―――――――――――――――――――――――(3分)
是奇函数. ―――――――――――――――――――――――(3分)
有 的对称中心为
的对称中心为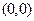 ,依题
,依题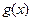 有对称中心
有对称中心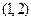 , ――――――――――(4分)
, ――――――――――(4分)
故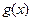 极大+
极大+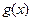 极小=4. ―――――――――――――――――――――――――(6分)
极小=4. ―――――――――――――――――――――――――(6分)
(II)由题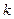 是该直线的斜率,令切点
是该直线的斜率,令切点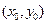 , ―――――――――――――-(7分)
, ―――――――――――――-(7分)
从而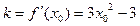 . ―――――――――――――――――――――――(9分)
. ―――――――――――――――――――――――(9分)
而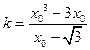 ,即
,即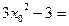
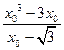 , ―――――――――――――――(10分)
, ―――――――――――――――(10分)
解得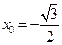 ,而当
,而当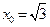 时也满足题意. ――――――――――――――――(11分)
时也满足题意. ――――――――――――――――(11分)
这样,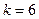 或
或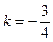 . ――――――――――――――――――――――――(12分)
. ――――――――――――――――――――――――(12分)
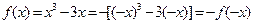 , ――――――――(2分)
, ――――――――(2分)又
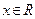 ,故
,故 是奇函数. ―――――――――――――――――――――――(3分)
是奇函数. ―――――――――――――――――――――――(3分)有
 的对称中心为
的对称中心为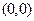 ,依题
,依题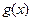 有对称中心
有对称中心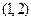 , ――――――――――(4分)
, ――――――――――(4分)故
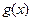 极大+
极大+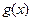 极小=4. ―――――――――――――――――――――――――(6分)
极小=4. ―――――――――――――――――――――――――(6分)(II)由题
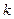 是该直线的斜率,令切点
是该直线的斜率,令切点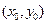 , ―――――――――――――-(7分)
, ―――――――――――――-(7分)从而
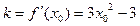 . ―――――――――――――――――――――――(9分)
. ―――――――――――――――――――――――(9分)而
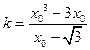 ,即
,即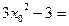
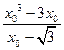 , ―――――――――――――――(10分)
, ―――――――――――――――(10分)解得
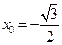 ,而当
,而当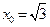 时也满足题意. ――――――――――――――――(11分)
时也满足题意. ――――――――――――――――(11分)这样,
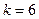 或
或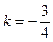 . ――――――――――――――――――――――――(12分)
. ――――――――――――――――――――――――(12分)
练习册系列答案
相关题目
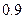 万元,汽车的维修费是第一年
万元,汽车的维修费是第一年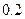 万元,以后逐年递增
万元,以后逐年递增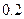 万元,问该品牌汽车使用多少年时,它的年平均费用最少?
万元,问该品牌汽车使用多少年时,它的年平均费用最少?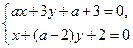 ,并对解的情况进行讨论.
,并对解的情况进行讨论.
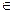 D,使得当x
D,使得当x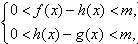 则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=
则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=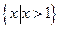 的四组函数如下:
的四组函数如下: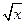 ; ②f(x)=10-x+2,g(x)=
; ②f(x)=10-x+2,g(x)= 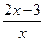 ;
;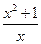 ,g(x)=
,g(x)= 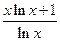 ; ④f(x)=
; ④f(x)= 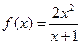 ,g(x)=2(x-1-e-x).
,g(x)=2(x-1-e-x).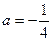 ”是“函数
”是“函数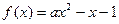 只有一个零点”的( )
只有一个零点”的( )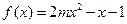 在区间
在区间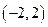 恰有一个零点,则
恰有一个零点,则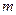 的取值范围是( )
的取值范围是( )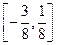
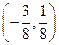
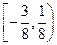
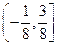
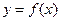 满足:
满足: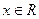 都有
都有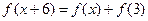 成立;
成立;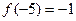 ;
;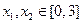 且
且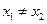 时,都有
时,都有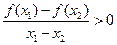 .
.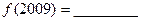 ;
;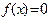 在区间
在区间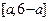 上恰有3个不同实根,则实数
上恰有3个不同实根,则实数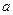 的取值范围是____.
的取值范围是____.