题目内容
【题目】在平面直角坐标系xOy中,直线l: 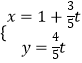 (t为参数),与曲线C:
(t为参数),与曲线C: ![]() (k为参数)交于A,B两点,求线段AB的长.
(k为参数)交于A,B两点,求线段AB的长.
【答案】解:(方法一)直线l的参数方程化为普通方程得4x﹣3y=4, 将曲线C的参数方程化为普通方程得y2=4x.
联立方程组 ![]() 解得
解得 ![]() ,或
,或 
所以A(4,4),B( ![]() ,﹣1).
,﹣1).
所以AB═ ![]() .
.
(方法二)将曲线C的参数方程化为普通方程得y2=4x.
直线l的参数方程代入抛物线C的方程得 ( ![]() t)2=4(1+
t)2=4(1+ ![]() ),即4t2﹣15t﹣25=0,
),即4t2﹣15t﹣25=0,
所以 t1+t2= ![]() ,t1t2=﹣
,t1t2=﹣ ![]()
所以AB=|t1﹣t2|= ![]() =
= ![]()
【解析】方法一:直线l的参数方程化为普通方程得4x﹣3y=4,将曲线C的参数方程化为普通方程得y2=4x.联立求出交点坐标,利用两点之间的距离公式即可得出.方法二:将曲线C的参数方程化为普通方程得y2=4x. 直线l的参数方程代入抛物线C的方程得 4t2﹣15t﹣25=0,利用AB=|t1﹣t2|= ![]() 即可得出.
即可得出.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
【题目】某舆情机构为了解人们对某事件的关注度,随机抽取了![]() 人进行调查,其中女性中对该事件关注的占
人进行调查,其中女性中对该事件关注的占![]() ,而男性有
,而男性有![]() 人表示对该事件没有关注.
人表示对该事件没有关注.
关注 | 没关注 | 合计 | |
男 |
| ||
女 | |||
合计 |
(1)根据以上数据补全![]() 列联表;
列联表;
(2)能否有![]() 的把握认为“对事件是否关注与性别有关”?
的把握认为“对事件是否关注与性别有关”?
(3)已知在被调查的女性中有![]() 名大学生,这其中有
名大学生,这其中有![]() 名对此事关注.现在从这
名对此事关注.现在从这![]() 名女大学生中随机抽取
名女大学生中随机抽取![]() 人,求至少有
人,求至少有![]() 人对此事关注的概率.
人对此事关注的概率.
附表:
|
|
|
|
|
|
|
|
|
|
|
|
![]()