题目内容
【题目】已知
为正项数列
的前n项和，且满足
.
(1)求出
，
(2)猜想
的通项公式并给出证明.
【答案】（1）
（2）
【解析】试题分析：（1）根据
，利用递推公式， 
代入即可求出
；（2）由（1）猜想
的通项公式，可由
，化简整理，即可得数列{an}是首项a1＝1，公差d＝1的等差数列，进而可得结论.
试题解析：（1）由Sn＝
＋
an(n∈N＋)（2）
可得a1＝
＋
a1，解得a1＝1，S2＝a1＋a2＝
＋
a2，解得a2＝2，
同理a3＝3，a4＝4，
（2）由（1）猜想an＝n.
证明：由Sn＝
＋
an ①
当n≥2时，Sn－1＝
＋
an－1， ②
①－②得(an－an－1－1)(an＋an－1)＝0，
∵an＋an－1≠0，∴an－an－1＝1，又a1＝1，故数列{an}是首项a1＝1，公差d＝1的等差数列，故
【题目】为了响应我市“创建宜居港城，建设美丽莆田”，某环保部门开展以“关爱木兰溪，保护母亲河”为主题的环保宣传活动，将木兰溪流经市区河段分成
段，并组织青年干部职工对每一段的南、北两岸进行环保综合测评，得到分值数据如下表：
南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
（Ⅰ）记评分在
以上（包括）为优良，从中任取一段，求在同一段中两岸环保评分均为优良的概率；
（Ⅱ）根据表中数据完成下面茎叶图；
（Ⅲ）分别估计两岸分值的中位数，并计算它们的平均值，试从计算结果分析两岸环保情况，哪边保护更好.
【题目】某校为了解校园安全教育系列活动的成效，对全校3000名学生进行一次安全意识测试，根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级，现随机抽取部分学生的答卷，统计结果及对应的频率分布直方图如下所示.
等级 | 不及格 | 及格 | 良好 | 优秀 |
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
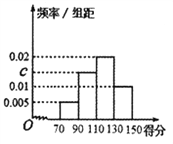
（1）求
的值；
（2）试估计该校安全意识测试评定为“优秀”的学生人数；
（3）已知已采用分层抽样的方法，从评定等级为“优秀”和“良好”的学生中任选6人进行强化培训；现再从这6人中任选2人参加市级校园安全知识竞赛，求选取的2人中有1人为“优秀”的概率；
