题目内容
【题目】某校为了解校园安全教育系列活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
等级 | 不及格 | 及格 | 良好 | 优秀 |
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
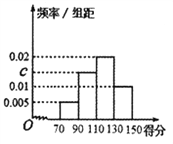
(1)求![]() 的值;
的值;
(2)试估计该校安全意识测试评定为“优秀”的学生人数;
(3)已知已采用分层抽样的方法,从评定等级为“优秀”和“良好”的学生中任选6人进行强化培训;现再从这6人中任选2人参加市级校园安全知识竞赛,求选取的2人中有1人为“优秀”的概率;
【答案】(1)![]() ,
,![]() .(2)600. (3)
.(2)600. (3)![]()
【解析】试题分析:(1)由频率分布直方图可知小长方形面积等于对应区间的概率(频率),所以可得得分在![]() 的频率,再根据频数等于总数与频率的乘积得
的频率,再根据频数等于总数与频率的乘积得![]() ,另根据对应比例关系有
,另根据对应比例关系有![]() ,解方程组可得
,解方程组可得![]() 的值;(2)由频率分布直方图可知小长方形面积等于“优秀”区间的概率(频率),所以可得“优秀”的频率,再根据频数等于总数与频率的乘积得“优秀”的人数;(3)根据分成抽样可得故选取的6人中“良好”有4人,“优秀”有2人,再根据枚举法确定从这6人中任选2人的基本事件总数以及选取的2人中有1人为“优秀”的所包含的基本事件数,最后根据古典概型概率求法求概率.
的值;(2)由频率分布直方图可知小长方形面积等于“优秀”区间的概率(频率),所以可得“优秀”的频率,再根据频数等于总数与频率的乘积得“优秀”的人数;(3)根据分成抽样可得故选取的6人中“良好”有4人,“优秀”有2人,再根据枚举法确定从这6人中任选2人的基本事件总数以及选取的2人中有1人为“优秀”的所包含的基本事件数,最后根据古典概型概率求法求概率.
试题分析:解:(1)由频率分布直方图可知,得分在![]() 的频率为
的频率为![]() ,
,
再由![]() 内的频数6,可知抽取的学生答卷数为60人,
内的频数6,可知抽取的学生答卷数为60人,
则![]() ,得
,得![]() ;
;
又由频率分布直方图可知,得分在![]() 的频率为0.2,即
的频率为0.2,即![]() ,
,
解得![]() .
.
进而求得![]() .
.
(2)由频率分布直方图可知,得分在![]() 的频率为0.2,
的频率为0.2,
由频率估计概率,可估计从全校答卷中任取一份,抽到“优秀”的概率为0.2,
设该校测试评定为“优秀”的学生人数为![]() ,则
,则![]() ,解得
,解得![]() ,
,
所以该校测试评定为“优秀”的学生人数约为600.
(3)“良好”与“优秀”的人数比例为24:12=2:1,
故选取的6人中“良好”有4人,“优秀”有2人,
“良好”抽取4人,记为![]() ,“优秀”抽取2 人,记为
,“优秀”抽取2 人,记为![]() ,
,
则从这6人中任取2人,所有基本事件如下:
![]() 共15个,
共15个,
事件![]() :“所抽取的2人中有人为‘优秀’”含有8个基本事件,
:“所抽取的2人中有人为‘优秀’”含有8个基本事件,
所以所求概率![]() .
.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注: 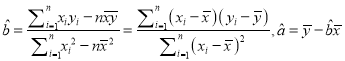 )
)
【题目】莫言是中国首位获得诺贝尔文学奖的文学家,国人欢欣鼓舞。某高校文学社从男女生中各抽取50名同学调查对莫言作品的了程度,结果如下:
阅读过莫言的作品数(篇) | 0~25 | 26~50 | 51~75 | 76~100 | 101~130 |
男生 | 3 | 6 | 11 | 18 | 12 |
女生 | 4 | 8 | 13 | 15 | 10 |
(1)试估计该学校学生阅读莫言作品超过50篇的概率.
(2)对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”,否则为“一般了解”,根据题意完成下表,并判断能否有![]() 的把握认为“对莫言作品的非常了解”与性别有关?
的把握认为“对莫言作品的非常了解”与性别有关?
非常了解 | 一般了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
注:K2=
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
年份200 | 0 | 1 | 2 | 3 | 4 |
人口数 | 5 | 7 | 8 | 11 | 19 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)据此估计2005年该城市人口总数.
参考公式: 用最小二乘法求线性回归方程系数公式 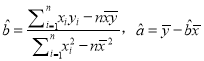
【题目】宁夏某市2008年至2012年新建商品住宅每平方米的均价![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 |
年份序号x | 1 | 2 | 3 | 4 | 5 |
每平米均价y | 2.0 | 3.1 | 4.5 | 6.5 | 7.9 |
(Ⅰ)求y关于x的线性回归方程![]() ;
;
(Ⅱ)利用(Ⅰ)中的回归方程,分析从2008年到2012年该市新建商品住宅每平方米均价的变化情况,并预测该市2015年新建商品住宅每平方米的均价.
附:回归直线的斜率和截距的最小二乘估计公式分别为
 ,
, ![]()
