Question

【题目】已知是定义在上的奇函数，且，若，时，有成立.

（Ⅰ）判断在上的单调性，并证明；

（Ⅱ）解不等式；

（Ⅲ）若对所有的恒成立，求实数的取值范围.

Answer 1

【答案】（1）减函数（2）（3）或或.

【解析】试题分析：

（Ⅰ）根据单调性定义，设，作差，由奇函数的定义化为，再利用已知条件得，从而得函数为减函数；

（Ⅱ）由减函数的定义得，但还要注意定义域，因此有；

（Ⅲ）题设不等式恒成立，即恒成立，在恒成立，作为的一次不等式，只要和时不等式成立即可．

试题解析：

（Ⅰ）在上是减函数，

任取且，则，

为奇函数，

，

由题知，，

，即，

在上单调递减.

（Ⅱ）在上单调递减，

，

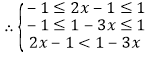解得不等式的解集为.

（Ⅲ），在上单调递减，

在上，，

问题转化为，即，对任意的恒成立，

令，即，对任意恒成立，

则由题知，解得或或.