题目内容
设数列a1,a2,…,an,…的前n项的和Sn与an的关系是Sn=kan+1,(其中k是与n无关的常数,且k≠1).(1)试写出用n,k表示的an的表达式;
(2)若
| lim | n→∞ |
分析:(1)由前n项的和Sn与an的关系 an+1=Sn+1-Sn,得到数列的递推公式,注意分析k是否为零,再求数列的通项公式.
(2)利用极限的值和第(1)的结果,代入sn整理出关于k的式子,再求k的值.
(2)利用极限的值和第(1)的结果,代入sn整理出关于k的式子,再求k的值.
解答:解:(1)∵Sn=kan+1,
∴an+1=Sn+1-Sn=(kan+1+1)-(kan+1),
∴an+1=kan+1-kan,即 (k-1)an+1=kan,
∵k≠1解得an+1=
an(1)
若k≠0,则由题设知a1≠0,由(1)式易知an≠0,n≥1,
∴
=
故该数列是公比为
的等比数列,
其首项为a1=S1=ka1+1,a1=
∴an=
(
)n-1=-
.
当k=0时,由(1)式知an=0,上式当n≥1时对k=0也成立.
(2)若
Sn=1,即
(kan+1)=1,
kan=
(Sn-1)=0,即
k•
=0,
∴
(
)n=0,∴|
|<1,解得k<
.
∴k的范围:k<
∴an+1=Sn+1-Sn=(kan+1+1)-(kan+1),
∴an+1=kan+1-kan,即 (k-1)an+1=kan,
∵k≠1解得an+1=
| k |
| k-1 |
若k≠0,则由题设知a1≠0,由(1)式易知an≠0,n≥1,
∴
| an+1 |
| an |
| k |
| k-1 |
| k |
| k-1 |
其首项为a1=S1=ka1+1,a1=
| 1 |
| 1-k |
∴an=
| 1 |
| 1-k |
| k |
| k-1 |
| kn-1 |
| (k-1)n |
当k=0时,由(1)式知an=0,上式当n≥1时对k=0也成立.
(2)若
| lim |
| n→∞ |
| lim |
| n→∞ |
| lim |
| n→∞ |
| lim |
| n→∞ |
| lim |
| n→∞ |
| -kn-1 |
| (k-1)n |
∴
| lim |
| n→∞ |
| k |
| k-1 |
| k |
| k-1 |
| 1 |
| 2 |
∴k的范围:k<
| 1 |
| 2 |
点评:本题由前n项和公式和sn和an的关系式,求出递推公式,然后求数列的通项公式;再由所给的极限值求k的范围.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
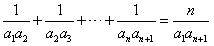 。
。