题目内容
3.向平面区域{(x,y)|0≤x≤2,0≤y≤2}内随机投入一点,则该点落在曲线y=$\frac{1}{x}$(x>0)下方的概率为$\frac{1+2ln2}{4}$.分析 平面区域{(x,y)|0≤x≤2,0≤y≤2},表示正方形,面积为4,求出曲线y=$\frac{1}{x}$(x>0)下方,在正方形内的面积,即可求出概率.
解答 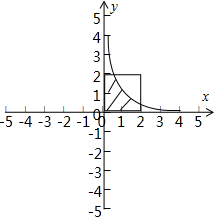 解:平面区域{(x,y)|0≤x≤2,0≤y≤2},表示正方形,面积为4,
解:平面区域{(x,y)|0≤x≤2,0≤y≤2},表示正方形,面积为4,
曲线y=$\frac{1}{x}$(x>0)下方,在正方形内的面积为$\frac{1}{2}×2$+${∫}_{\frac{1}{2}}^{2}\frac{1}{x}dx$=1+2ln2,
所以该点落在曲线y=$\frac{1}{x}$(x>0)下方的概率为$\frac{1+2ln2}{4}$.
故答案为:$\frac{1+2ln2}{4}$.
点评 本题考查了几何概率问题,考查学生的计算能力,确定区域的面积是关键.

练习册系列答案
相关题目
13. 一机器元件的三视图及尺寸如图所示(单位:dm),则该组合体的体积为( )
一机器元件的三视图及尺寸如图所示(单位:dm),则该组合体的体积为( )
 一机器元件的三视图及尺寸如图所示(单位:dm),则该组合体的体积为( )
一机器元件的三视图及尺寸如图所示(单位:dm),则该组合体的体积为( )| A. | 80dm3 | B. | 88dm3 | C. | 96dm3 | D. | 112dm3 |
8.i为虚数单位,复数z=i2012+i2015在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.
四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.