题目内容
(本题12分)
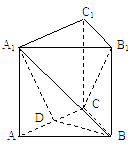 如图,正三棱柱ABC-A1B1C1的底面边长是2, 侧棱长是, D为AC的中点.
如图,正三棱柱ABC-A1B1C1的底面边长是2, 侧棱长是, D为AC的中点.
(1)求证: B1C∥平面A1BD
(2)求二面角A1-BD-A的大小.
(3)求直线AB1与平面A1BD所成角的大小.
(2) 60° (3) ∠AOH=arcsin
解析:
法1: 如图所示(1)设A1B与AB1交于O点, 在△AB1C中, OD为其中位线,
 ∴OD∥B1C, ODÌ平面A1BD, B1CÌ平面A1BD, ∴B1C∥平面A1BD
∴OD∥B1C, ODÌ平面A1BD, B1CÌ平面A1BD, ∴B1C∥平面A1BD
(2) ∵D是AC的中点, △ABC为正三角形, ∴BD⊥AC, 三棱柱ABC-A1B1C1为正三棱柱, ∴ A1A⊥BD, ∴BD⊥平面A1AD, ∴BD⊥A1D, BD⊥AD, ∴∠A1DA为二面角A1-BD-A的平面角, A1A=, AD=1, tan∠A1DA= = , ∴∠A1DA= 60°. ∴二面角A1-BD-A的平面角为60°.
(3)∵ BD⊥平面A1AD, BDÌ平面A1BD, ∴平面A1AD⊥平面A1BD, 过A作AH⊥A1D于H点,∴AH⊥平面A1BD, ∴∠AOH为直线AB1与平面A1BD所成角, 在Rt△A1AD中AH== ![]() = , AO= sin∠AOH= =
= , AO= sin∠AOH= = ![]() = , ∠AOH=arcsin.
= , ∠AOH=arcsin.
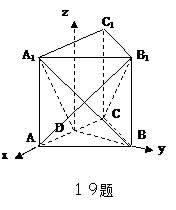
法2: (空间向量法)建坐标系如图, 则
A(1,0,0), D(0,0,0), B(0,, 0), A1(1, 0, ) B1(0, , ) , C(-1,0,0)
![]() (1)
(1) ![]() =(1, 0, ),
=(1, 0, ), ![]() =(0,, 0),
=(0,, 0), ![]() =(1, , ) , ∴
=(1, , ) , ∴ ![]() =
=![]() +
+ ![]() , ∴
, ∴![]() 、
、![]() 、
、![]() 共面, 又∵CB1Ì平面A1BD, ∴B1C∥平面A1BD
共面, 又∵CB1Ì平面A1BD, ∴B1C∥平面A1BD
(2) 平面ABD的法向量设为![]() =(0,0,1), 平面A1BD的法向量为
=(0,0,1), 平面A1BD的法向量为![]() =(x,y,z),
=(x,y,z),
∵ 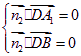 ,
,
∴ 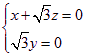 , y=0, 令z=1, 则x=-, ∴
, y=0, 令z=1, 则x=-, ∴![]() =(-,0,1) ,
=(-,0,1) ,
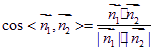 =
=
∴ 二面角A1-BD-A的大小的60°.
(3) 直线AB1与平面A1BD所成角θ, 则![]() =(-1, , ),平面A1BD的法向量为
=(-1, , ),平面A1BD的法向量为![]() =(-,0,1) , sinθ=
=(-,0,1) , sinθ=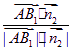 = = , ∴ θ=arcsin.
= = , ∴ θ=arcsin.

 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
 中,
中,  ,点
,点 是棱
是棱 上一点.
上一点.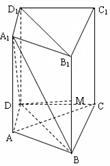
 面
面 ;
; ;
; 中,
中,  ,点
,点 是棱
是棱 上一点
上一点 面
面 ;
; ;
;
 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.