题目内容
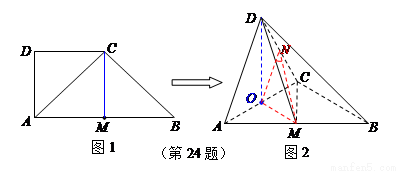
(本题12分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点,将△ACD沿 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求二面角A-CD-M的余弦值.
【答案】
解:(Ⅰ)取AC的中点O,连接DO,则DO⊥AC,
∵平面ADC⊥平面ABC,∴DO⊥平面ABC,∴DO⊥BC,
在直角梯形ABCD中,连接CM,可得CM=AD=2,AC=BC=2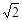 ,
,
∴AC2+BC2=AB2,∴AC⊥BC,
又∵DO∩AC=O,∴BC⊥平面ACD;
(Ⅱ)取CD的中点N,连接MO, NO, MN,
则MO∥BC,∴MO⊥平面ACD,∴MO⊥CD,
∵AD⊥CD,ON∥AD,∴ON⊥CD,又∵MO∩NO=O,
∴CD⊥平面MON,∴CD⊥MN,∴∠MNO是所求二面角的平面角
在Rt△MON中,MO=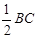 =
=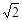 ,NO=
,NO=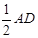 =1,
=1,
∴MN=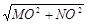 =
=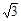 ,∴cos∠MNO=
,∴cos∠MNO=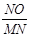 =
=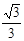
【解析】略

练习册系列答案
相关题目

 中,
中,  ,点
,点 是棱
是棱 上一点.
上一点.
 面
面 ;
; ;
; 平面PCD;(2)求证:平面PCE⊥平面PCD.
平面PCD;(2)求证:平面PCE⊥平面PCD.
