题目内容
(本题12分)如图,在侧棱锥垂直底面的四棱锥ABCD-A1B1C1D1中,AD∥BC,
AD⊥AB,AB= 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
与直线AA1的交点。
(1)证明:(i)EF∥A1D1;
(ii)BA1⊥平面B1C1EF;
(2)求BC1与平面B1C1EF所成的角的正弦值。

【答案】
(1)见解析;(2) BC与平面 所成角的正弦值是
所成角的正弦值是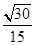 .
.
【解析】本试题主要是考查了线线平行的证明,以及线面垂直的证明,以及线面角的求解。
(1)因为在侧棱锥垂直底面的四棱锥ABCD-A1B1C1D1中,AD∥BC,
AD⊥AB,AB=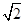 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
与直线AA1的交点。那么可知得到证明。
(2)先证明垂直于平面内的两条相交直线即可。
(3)根据上一问可知线面垂直,那么利用平面的垂直,得到斜线的射影,进而表示线面角的大小,求解得到。
(1)(i)因为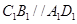 ,
,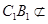 平面ADD1 A1,所以
平面ADD1 A1,所以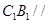 平面ADD1 A1.
平面ADD1 A1.
又因为平面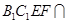 平面ADD1 A1=
平面ADD1 A1=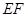 ,所以
,所以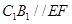 .所以
.所以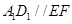 . 3分
. 3分
(ⅱ)因为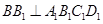 ,所以
,所以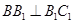 ,
,
又因为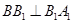 ,所以
,所以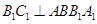 ,
,
在矩形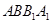 中,F是AA的中点,
中,F是AA的中点,
即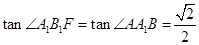 .
.
即 ,故
,故 .所以
.所以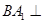 平面
平面 . 4分
. 4分
(2) 设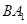 与
与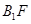 交点为H,连结
交点为H,连结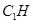 .
.
由(1)知 ,所以
,所以 是
是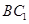 与平面
与平面 所成的角. 在矩形
所成的角. 在矩形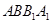 中,
中,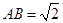 ,
,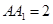 ,得
,得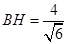 ,在直角
,在直角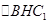 中,
中,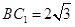 ,
,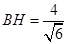 ,得
,得
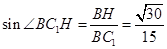 ,所以BC与平面
,所以BC与平面 所成角的正弦值是
所成角的正弦值是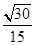 .
5分
.
5分

练习册系列答案
相关题目
 中,
中,  ,点
,点 是棱
是棱 上一点.
上一点.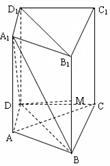
 面
面 ;
; ;
; 中,
中,  ,点
,点 是棱
是棱 上一点
上一点 面
面 ;
; ;
;
 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.